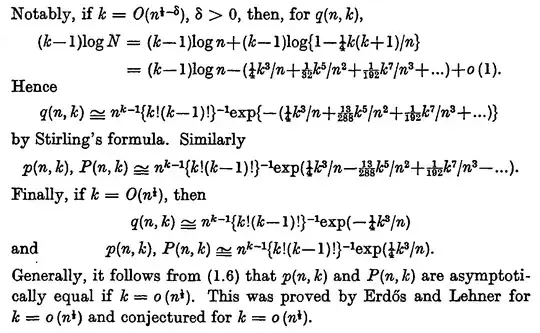In number theory and combinatorics, a partition of a positive integer $n$, also called an integer partition, is a way of writing $n$ as a sum of positive integers. Partitions into distinct parts are sometimes called "strict partitions". Is there a polynomial upper bound for the strict partition on $K$ summands?
-
What kind of upper bound do you want? $n^K$ is a trivial upper bound if you want any. – Dec 31 '16 at 04:42
-
Thanks!! I change the question!! – Frank Vega Dec 31 '16 at 04:44
-
1As you may know, strict partitions correspond bijectively to partitions into odd parts. – Servaes Dec 31 '16 at 04:51
-
According to https://oeis.org/A000009 the number $q(n)$ of strict partitions of $n$ grows exponentially; asymptotically $$q(n) \sim \frac{\exp(\pi\sqrt{n/3-1/72})}{4\sqrt[4]{3(n-1/24)^3}}.$$ – Servaes Dec 31 '16 at 04:52
2 Answers
Here is a computational approach to the problem. Recall the discussion from the following MSE link where the formula
$$[z^n] Z(P_k)\left(\frac{z}{1-z}\right)$$
was applied and a recurrence for $Z(P_k)$ was given. As an example consider $Z(P_5)$ which is
$$Z(P_5) = {\frac {{a_{{1}}}^{5}}{120}}-1/12\,a_{{2}}{a_{{1}}}^{3} +1/6\,a_{{3}}{a_{{1}}}^{2}+1/8\,a_{{1}}{a_{{2}}}^{2} \\-1/4\,a_{{4}}a_{{1}}-1/6\,a_{{2}}a_{{3}}+1/5\,a_{{5}}$$
The substituted cycle index then becomes
$$Z(P_5)\left(\frac{z}{1-z}\right) = {\frac {{z}^{5}}{120\, \left( 1-z \right) ^{5}}}-1/12\,{\frac {{z}^ {5}}{ \left( -{z}^{2}+1 \right) \left( 1-z \right) ^{3}}} \\+1/6\,{ \frac {{z}^{5}}{ \left( -{z}^{3}+1 \right) \left( 1-z \right) ^{2} }}+1/8\,{\frac {{z}^{5}}{ \left( 1-z \right) \left( -{z}^{2}+1 \right) ^{2}}}-1/4\,{\frac {{z}^{5}}{ \left( -{z}^{4}+1 \right) \left( 1-z \right) }} \\-1/6\,{\frac {{z}^{5}}{ \left( -{z}^{2}+1 \right) \left( -{z}^{3}+1 \right) }}+1/5\,{\frac {{z}^{5}}{-{z}^{ 5}+1}}.$$
We proceed to an important observation. Suppose we convert the substituted cycle index as shown in the example to its maximal partial fraction decomposition (which means going to complex roots, and these are all roots of unity). We seek to extract the coefficient on $[z^n].$ Considering a particular term from the partial fraction decomposition we have with $\zeta$ a root of unity that
$$[z^n] \frac{z^q}{(z-\zeta)^p} = [z^{n-q}] \frac{1}{\zeta^p} \frac{1}{(z/\zeta-1)^p} = (-1)^p \frac{1}{\zeta^p} {n-q+p-1\choose p-1} \zeta^{-(n-q)}.$$
Note furthermore that on adding $\lambda = \mathrm{lcm}(1,2,\ldots,k)$ to $n$ all roots of unity have simultaneously returned to their value at $n$ and this is the smallest offset to produce this phenomenon. The powers of the different $\zeta$ have morphed into a constant, and we obtain a polynomial from the binomial coefficients. The degree of the polynomial is $k-1$ as obtained from the term $a_1^k/k! = (z/(1-z))^k/k!.$ Therefore we immediately conclude that $Q_{n,k}$ (notation from the cited post) is asymptotic to $n^{k-1}$ with a constant to be determined.
We can compute these polynomials by interpolating using the values of $Q_{n,k}$ from the recurrence. We get $\lambda$ different formulae / cases, each of degree $k-1.$ The following Maple code does this.
Q :=
proc(n, k)
option remember;
if n=0 and k=0 then return 1 fi;
if n=0 or k=0 then return 0 fi;
if k=1 then return 1 fi;
if n < 1/2*k*(k+1) then return 0 fi;
1/k*add((-1)^(q-1)*
add(Q(n-(p+1)*q, k-q), p=0..floor(n/q)-1),
q=1..k);
end;
PSEQ :=
proc(k)
option remember;
local n, lambda, l, res, locs, vals;
res := [];
lambda := lcm(seq(q, q=1..k));
for l from 1 to lambda do
locs := [seq(l+p*lambda, p=0..k-1)];
vals := map(loc -> Q(loc, k), locs);
res :=
[op(res),
unapply(interp(locs, vals, n), n)];
od;
res;
end;
X :=
proc(n, k)
local Fseq, lambda, idx;
Fseq := PSEQ(k);
lambda := nops(Fseq);
idx := n mod lambda;
if idx = 0 then idx := idx + lambda; fi;
op(idx, Fseq)(n);
end;
SIM := (n,k)->binomial(n-1,k-1)/k!;
This will produce the following sequence of polynomials for $k=5,$ listed according to the remainder upon division by $\mathrm{lcm}(1,2,3,4,5)= 60$ starting with remainder one (zero residue represented by $\lambda.$)
> PSEQ(5);
4 3 31 2 41 949
[n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11 203
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 24 360
4 3 31 2 41 181
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 320
4 3 31 2 11 31
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 45
4 3 31 2 41 305
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 576
4 3 31 2 11 27
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 40
4 3 31 2 41 1309
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11 31
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 45
4 3 31 2 41 141
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 320
4 3 31 2 11 55
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 72
4 3 31 2 41 1309
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11
n -> 1/2880 n - 1/96 n + --- n - -- n + 4/5,
288 24
4 3 31 2 41 949
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11 203
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 24 360
4 3 31 2 41 49
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 96 64
4 3 31 2 11 31
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 45
4 3 31 2 41 949
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11 27
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 40
4 3 31 2 41 1309
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11
n -> 1/2880 n - 1/96 n + --- n - -- n + 8/9,
288 24
4 3 31 2 41 141
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 320
4 3 31 2 11 203
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 24 360
4 3 31 2 41 1309
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11
n -> 1/2880 n - 1/96 n + --- n - -- n + 4/5,
288 24
4 3 31 2 41 305
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 576
4 3 31 2 11 203
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 24 360
4 3 31 2 41 181
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 320
4 3 31 2 11 31
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 45
4 3 31 2 41 949
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11
n -> 1/2880 n - 1/96 n + --- n - -- n + 7/8,
288 24
4 3 31 2 41 1309
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11 31
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 45
4 3 31 2 41 141
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 320
4 3 31 2 11 203
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 24 360
4 3 31 2 41 377
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 576
4 3 31 2 11
n -> 1/2880 n - 1/96 n + --- n - -- n + 4/5,
288 24
4 3 31 2 41 949
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11 203
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 24 360
4 3 31 2 41 181
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 320
4 3 31 2 11
n -> 1/2880 n - 1/96 n + --- n - -- n + 8/9,
288 24
4 3 31 2 41 949
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11 27
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 40
4 3 31 2 41 1309
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11 31
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 45
4 3 31 2 41 41
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 96 64
4 3 31 2 11 203
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 24 360
4 3 31 2 41 1309
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11
n -> 1/2880 n - 1/96 n + --- n - -- n + 4/5,
288 24
4 3 31 2 41 949
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11 55
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 72
4 3 31 2 41 181
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 320
4 3 31 2 11 31
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 45
4 3 31 2 41 949
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11 27
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 40
4 3 31 2 41 377
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 576
4 3 31 2 11 31
n -> 1/2880 n - 1/96 n + --- n - -- n + --,
288 24 45
4 3 31 2 41 141
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 96 320
4 3 31 2 11 203
n -> 1/2880 n - 1/96 n + --- n - -- n + ---,
288 24 360
4 3 31 2 41 1309
n -> 1/2880 n - 1/96 n + --- n - -- n + ----,
288 96 2880
4 3 31 2 11
n -> 1/2880 n - 1/96 n + --- n - -- n + 1]
288 24
Surprise! We are now able to compute $Q_{n,8}$ with $n$ from $16000$ to $16008$ which is out of reach of the recurrence and we get
$$1310588091362349970144, 1311162227425710083350, \\ 1311736579060069106145, 1312311146331986804908, \\ 1312885929309812275982, 1313460928060138717214, \\ 1314036142651349327782, 1314611573150070750093, \\ 1315187219624720299308,\ldots$$
Extracting the leading coefficients we obtain the sequence
> seq(lcoeff(op(1,PSEQ(k))(n)), k=1..8);
1, 1/2, 1/12, 1/144, 1/2880, 1/86400, 1/3628800, 1/203212800
This is OEIS A010790 or
$$(k-1)! \times k!.$$
What this says is that the dominant asymptotic originates with $a_1^k/k!$ which gives
$$\frac{1}{k!} [z^n] \frac{z^k}{(1-z)^k} = \frac{1}{k!} [z^{n-k}] \frac{1}{(1-z)^k} = \frac{1}{k!} {n-k+k-1\choose k-1} \\ = \frac{1}{(k-1)! \times k!} (n-1)^{\underline{k-1}}.$$
We thus finally conjecture that
$$\bbox[5px,border:2px solid #00A000]{ Q_{n,k} \sim \frac{1}{(k-1)! \times k!} (n-1)^{\underline{k-1}}.}$$
This post received some basic input from mathpages.com.
- 61,317
-
-
Thank you! I recall you saying you were interested in learning more about cycle indices. – Marko Riedel Jan 01 '17 at 22:58
-
If $K$ is fixed, yes. The paper An Asymptotic Formula in the Theory of Partitions by G Szekeres states both an upper and lower bound using the notation "$q(n,k)$, the number of partitions of $n$ into exactly $k$ positive unequal parts."

If $K$ grows with $n$, then no. The same paper goes on to describe the case where $K$ is allowed to grow with $n$ up to $K = O(\sqrt{n})$.
And in a follow-up paper, Some Asymptotic Formulae in the Theory of Partitions (II) by G. Szekeres, he identifies the $K$ which maximizes $q(n, K)$ asymptotically as $n$ tends to infinity.
- 181