4

I am working on a proof about Dedekind cuts on the positive rational numbers. I have been stuck for a while on the following point and would appreciate any help.

Given $x\in \mathbb{Q}^+$ such that $x^2<2$, how to find $y\in \mathbb{Q}^+$ such $y>x$ and $y^2<2$?

Dan Christensen
  • 14,529

3 Answers3

3

Note that if $0<\epsilon<1$, then $$(x+\epsilon)^2=x^2+2x\epsilon+\epsilon^2<x^2+(2x+1)\epsilon.$$ If you want $(x+\epsilon)^2$ to be less than $2$, you can choose $\epsilon$ such that $x^2+(2x+1)\epsilon\leq 2$, which is equivalent to $\epsilon\leq\frac{2-x^2}{2x+1}$.

So to find your $y$, just pick $\epsilon>0$ such that $\epsilon<\min\left(\frac{2-x^2}{2x+1},1\right)$ and take $y=x+\epsilon$.

Eric Wofsey
  • 330,363
  • If $x\le 1$ then could we use $y=1.1$; otherwise $y=x+\frac{2-x^2}{2x+1}$? – Dan Christensen Dec 24 '16 at 15:39
  • Yes, I believe that should work. – Eric Wofsey Dec 24 '16 at 19:05
  • I thought I understood, but still can't complete this part of the proof for $x>1$. I can't prove that $y^2 <2$ (as I have defined $x$ and $y$ here). – Dan Christensen Dec 28 '16 at 05:58
  • Just follow what I wrote, setting $\epsilon=\frac{2-x^2}{2x+1}$. – Eric Wofsey Dec 28 '16 at 06:12
  • But how to prove $y^2<2$? – Dan Christensen Dec 28 '16 at 06:16
  • $y^2=(x+\epsilon)^2<x^2+(2x+1)\epsilon=x^2+(2-x^2)=2$. – Eric Wofsey Dec 28 '16 at 06:17
  • Why is $(2x+1)\epsilon = 2-x^2$? – Dan Christensen Dec 28 '16 at 16:10
  • I think I get it! For $0< \epsilon < 1$, choosing $\epsilon$ such that $x^2 +(2x+1)\epsilon = 2$ or $\epsilon = \frac{2-x^2}{2x+1}$ will guarantee that $(x+\epsilon)^2<2$. I will mull this over, and run it through my proof checker just to be sure. – Dan Christensen Dec 28 '16 at 18:20
  • I still don't see how to structure a formal proof. Using only arithmetic on $Q^+$, I want to prove: $\forall x\in Q^+: [x^2 < 2 \to \exists y\in Q^+: [y>x \land y^2 < 2]]$. I can only think of starting by assuming that $x^2<2$, then considering two or more cases depending only on $x$ (which cases?) and showing that in each case we have $\exists y\in Q^+: [y>x \land x^2 < 2]$. You mention only one "case": $0<\epsilon < 1$ which would not depend on $x$. – Dan Christensen Dec 28 '16 at 20:36
  • 2
    I wrote the proof "backwards" to make the motivation behind it easier to understand, but apparently that was the opposite of what you wanted. I honestly can't tell what difficulty you're having: just pick $\epsilon$ such that $\epsilon\leq \frac{2-x^2}{2x+1}$ and $0<\epsilon<1$, and then plug it into the calculation I did at the beginning. – Eric Wofsey Dec 28 '16 at 20:41
  • 1
    By the way, this works for every positive rational number $q$ in exactly the same way. – egreg Dec 29 '16 at 16:33
  • @EricWofsey It seems to me that the strict inequality $\epsilon < \frac{2-x^2}{2x+1}$ would also work. Have I missed something? – Dan Christensen Dec 29 '16 at 18:01
  • Yes, that would work, because $\epsilon<\frac{2-x^2}{2x+1}$ implies $\epsilon\leq\frac{2-x^2}{2x+1}$... – Eric Wofsey Dec 29 '16 at 20:20
  • @EricWofsey It works! Thank you for your patience. I should be able to post a full formal proof sometime in January -- I hope. – Dan Christensen Dec 30 '16 at 06:54
  • My proof to this point, has hinged on constructing the set $S={\epsilon \in Q^+: \epsilon < 1 \land \epsilon < \frac{2-x^2}{2x+1}}$ and proving it non-empty. Then any element $\epsilon \in S$ would work to give me $(x+\epsilon)^2<2$. – Dan Christensen Dec 30 '16 at 07:11
  • I probably didn't need to construct the set $S$, and just needed to prove the existence of $\epsilon \in Q^+$ such that $\epsilon < 1$ and $\epsilon < \frac{2-x^2}{2x+1}}$. In my next draft. – Dan Christensen Dec 30 '16 at 07:27
3

The Stern-Brocot tree is one of my favorite tools. It is assumed to be well-known in what follows. Let $m$ and $n$ be positive integers. Initialize (zeroth iteration): $$ x = \frac{m}{n} < \sqrt{2} \quad ; \quad y = 2/x = \frac{2n}{m} > \frac{2}{\sqrt{2}} \quad \Longrightarrow \quad y > \sqrt{2} $$ Now walk through the Stern-Brocot tree iteratively until $\,y < \sqrt{2}$ . From the properties of the tree, we know that always will be $\,y > x$ . First iteration: $$ y := \frac{m+2n}{n+m} = \frac{x+2}{x+1} < \sqrt{2} \quad \mbox{?} $$ No, because a contradiction with $\,x<\sqrt{2}\,$ is derived: $$ (x+2)^2 < 2(x+1)^2 \quad \Longleftrightarrow \quad x^2+4x+4 < 2x^2+4x+2 \quad \Longleftrightarrow \quad x^2 > 2 $$ Second iteration: $$ y := \frac{m+(m+2n)}{n+(n+m)} = \frac{2m+2n}{m+2n} = \frac{2x+2}{x+2} < \sqrt{2} \quad \mbox{?} $$ Yes, because: $$ (2x+2)^2 < 2(x+2)^2 \quad \Longleftrightarrow \quad 4x^2+8x+4 < 2x^2+8x+8 \quad \Longleftrightarrow \quad x^2 < 2 $$ So the outcome is: $$ y(x) = 2\frac{x+1}{x+2} $$ Check, check, double check .. If we are allowed to have an embedding of the rationals in the reals, then the derivative is: $$ y'(x) = \frac{2(x+2)-(2x+2)}{(x+2)^2} = \frac{2}{(x+2)^2} > 0 $$ And some function values are: $$ y(0) = 1 \quad ; \quad y(\sqrt{2}) = 2\frac{\sqrt{2}+1}{2+\sqrt{2}} = \sqrt{2} $$ But $y(x)$ is monotonically increasing, so $\sqrt{2}$ is the maximum at the interval $\left[0,\sqrt{2}\right]$ and all other values of $y(x)$ are smaller than this, but greater than $x$, as requested.

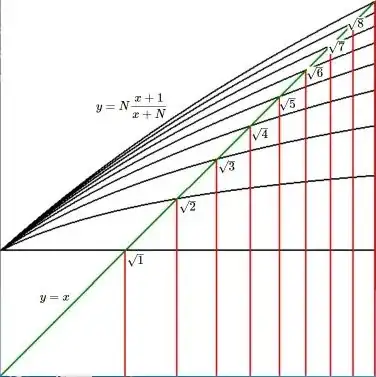
BONUS. Let $N$ be any positive integer. Now generalize the question as follows.
Given $x\in \mathbb{Q}^+$ such that $x^2 < N$, how to find $y\in \mathbb{Q}^+$ such that $y>x$ and $y^2 < N$ ?
It's left as an exercise for the reader to prove that this is a solution: $$ y(x) = N\frac{x+1}{x+N} $$ Can't resist to display some members of the $y$ - family in a $[0,3]\times[0,3]$ picture:

enter image description here

Han de Bruijn
  • 17,070
1

Here is an exercise (which is not too far from what @HanDeBruijn is doing) from Hardy's "A Course of Pure Mathematics", 3rd edition, page 12 enter image description here The book is old and should be freely available online.

Basically

  1. $\frac{m}{n}<\sqrt{2} \Rightarrow \sqrt{2} < \frac{m+2n}{m+n}$. $$\frac{m}{n}<\sqrt{2}=\frac{2-\sqrt{2}}{\sqrt{2}-1}\Rightarrow \\ m(\sqrt{2}-1)<n(2-\sqrt{2})\Rightarrow \\ \sqrt{2}(m+n)<m+2n$$
  2. Similarly if $\frac{m}{n}>\sqrt{2} \Rightarrow \sqrt{2} > \frac{m+2n}{m+n}$.
  3. $\left|\frac{m+2n}{m+n} - \sqrt{2}\right|< \left|\frac{m}{n} - \sqrt{2}\right|$. $$\left|\frac{\frac{m+2n}{m+n} - \sqrt{2}}{\frac{m}{n} - \sqrt{2}}\right|=\left|\frac{\frac{m+2n}{m+n} - \sqrt{2}}{\frac{m^2}{n^2} - 2}\cdot \left(\frac{m}{n} + \sqrt{2}\right)\right|\\=\left|\frac{n^2}{m^2 - 2n^2}\cdot \left(\frac{m+2n}{m+n} - \sqrt{2}\right)\cdot \left(\frac{m}{n} + \sqrt{2}\right)\right|\\=\left|\frac{n^2}{m^2 - 2n^2}\cdot \left( \frac{m^2+2mn}{nm+n^2} +\sqrt{2}\frac{m+2n}{m+n} -\sqrt{2}\frac{m}{n} -2 \right)\right|\\=\left|\frac{n^2}{m^2 - 2n^2}\cdot \left( \frac{m^2+2mn}{nm+n^2} - 2 +\sqrt{2}\left(\frac{m+2n}{m+n} -\frac{m}{n}\right) \right)\right|\\=\left|\frac{n^2}{m^2 - 2n^2}\cdot \left( \frac{m^2-2n^2}{nm+n^2} +\sqrt{2}\frac{2n^2-m^2}{nm+n^2} \right)\right|\\=\left|\frac{n^2}{nm+n^2}\cdot \left( 1-\sqrt{2} \right)\right|=\left|\frac{n^2}{nm+n^2}\right| \cdot \left| 1-\sqrt{2} \right|<1$$

And this process can be repeated, by taking $$m_1=m+2n \\n_1=m+n \\...\\m_{k+1}=m_k+2n_k \\n_{k+1}=m_k+n_k$$ considering alterations of course, jumping around $\sqrt{2}$ and becoming closer to $\sqrt{2}$ each step.

This will lead to $\frac{m}{n} < \frac{m_2}{n_2} < \sqrt{2} < \frac{m_1}{n_1}$ or $\frac{m^2}{n^2} < \frac{m_2^2}{n_2^2} < 2< \frac{m_1^2}{n_1^2}$. So if $x=\frac{m}{n}$ then the first suitable $y$ is $y=\frac{m_2}{n_2}$.

rtybase
  • 16,907
  • Indeed, more or less as has been done in this answer . However, those opposite directions and the jumping around are not wanted by the OP. – Han de Bruijn Dec 29 '16 at 15:25
  • @HandeBruijn true, that's why at least 2 iterations are required $x=\frac{m}{n}<\sqrt{2}$, then we ignore $\frac{m_1}{n_1}>\sqrt{2}$ and consider again $x=\frac{m}{n}<\frac{m_2}{n_2}<\sqrt{2}$, i.e. $y=\frac{m_2}{n_2}$ – rtybase Dec 29 '16 at 15:38