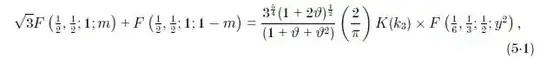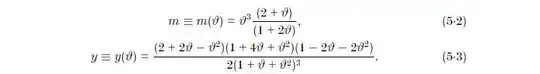How to show an infinite number of algebraic numbers $\alpha$ and $\beta$ for $_2F_1\left(\frac13,\frac13;\frac56;-\alpha\right)=\beta\,$?

Question

(Note: This is the case $a=\frac13$ of ${_2F_1\left(a ,a ;a +\tfrac12;-u\right)}=2^{a}\frac{\Gamma\big(a+\tfrac12\big)}{\sqrt\pi\,\Gamma(a)}\int_0^\infty\frac{dx}{(1+2u+\cosh x)^a}.\,$ There is also $a=\frac14$ and $a=\frac16$.)

In a post, Reshetnikov considered some integrals and the surprising evaluations, $$ \frac{1}{48^{1/4}\,K(k_3)}\,\int_0^1 \frac{dx}{\sqrt{1-x}\,\sqrt[3]{x^2+\color{blue}{4}x^3}}=\,_2F_1\big(\tfrac{1}{3},\tfrac{1}{3};\tfrac{5}{6};-\color{blue}{4}\big)= \frac3{5^{5/6}}\tag1$$

$$ \frac{1}{48^{1/4}\,K(k_3)}\,\int_0^1 \frac{dx}{\sqrt{1-x}\,\sqrt[3]{x^2+\color{blue}{27}x^3}}=\,_2F_1\big(\tfrac{1}{3},\tfrac{1}{3};\tfrac{5}{6};-\color{blue}{27}\big)=\frac{4}{7}\tag2$$

We postulate these are just the first of an infinite family of algebraic numbers $\alpha$ and $\beta$ such that,
$$_2F_1\left(\frac13,\frac13;\frac56;-\alpha\right)=\beta\tag3$$

$$\begin{array}{|c|c|c|c|c|} \hline p&\tau&\alpha&\beta&\text{Deg}\\ \hline 3&\frac{1+3\sqrt{-3}}2& \large \frac13& \large \frac{2}{3^{2/3}}&1\\ 5&\frac{1+5\sqrt{-3}}2&\color{blue}{4}& \large\frac3{5^{5/6}} &1\\ 7&\frac{1+7\sqrt{-3}}2&\color{blue}{27}&\large\frac47&1\\ 11&\frac{1+11\sqrt{-3}}2& \sqrt{11}\big(2\sqrt3 + \sqrt{11}\big)^3& \large\frac6{11^{11/12}} \frac1{U_{33}^{1/4}} &2 \\ 13&\frac{1+13\sqrt{-3}}2& 4\sqrt{13}\big(4 + \sqrt{13}\big)^3&\large\frac7{13}\frac1{U_{13}}&2\\ 17&\frac{1+17\sqrt{-3}}2& \frac4{729}\left[(1 + \sqrt[3]{17})^2 + 6\right]^6& \large\frac9{17^{5/6}}\left(\frac{18}{17^{1/3}}-7\right)^{1/3}&3\\ 19&\frac{1+19\sqrt{-3}}2& \frac1{27}\left[(1 + \sqrt[3]{19})^2 + 5\right]^6 &\large \frac{10}{19} \Big(1-\frac{(1-19^{1/3})^2}{3}\Big)&3\\ 29&\frac{1+29\sqrt{-3}}2& 4(u_1)^6&\frac{15}{29^{5/6}}(u_2)^{1/3} &5\\ 31&\frac{1+31\sqrt{-3}}2& \frac1{27}( v_1)^6 &\frac{16}{31} (v_2)&5\\ \hline \end{array}$$

and so on, where $U_{13} = \frac{3+\sqrt{13}}2$, $U_{33} = 23+4\sqrt{33}\,$ are fundamental units, while $u_i$ and $v_i$ are roots of quintics, etc. (While the quintics were solvable in radicals, unfortunately they don't have the simple form as the others. The original forms for $p=17,19$ were found by yours truly while alternative ones were suggested by Reshetnikov.) And $\text{Deg}$ is degree of $\alpha(\tau)$ and $\beta^6(\tau)$.

Conjecture 1: Let $\tau = \frac{1+p\sqrt{-3}}{2}$. Using the Dedekind eta function quotient $\lambda=\frac{\eta\big(\tfrac{\tau+1}{3}\big)}{\eta(\tau)}$, then $\alpha$ is just a quadratic, $$16\cdot27\,\alpha(1+\alpha)=\left( \lambda^6 -27\, \lambda^{-6} \right)^2$$ or more simply, $$\alpha = \frac1{4\sqrt{27}}\big(\lambda^3-\sqrt{27}\,\lambda^{-3}\big)^2\tag4$$ And if $p=6k\pm1$ is a prime, then $\alpha$ and $\beta^6$ of $(3)$ are algebraic numbers of degree $k$.

Alternatively, one can use the well-known j-function $j(\tau)$, $$j(\tau) = {1 \over q} + 744 + 196884 q + 21493760 q^2 + 864299970 q^3+\dots$$ which is easily calculated in Mathematica as 12^3KleinInvariantJ[tau].

Conjecture 2: Let $\tau = \frac{1+p\sqrt{-3}}{2}$. Then $\alpha$ is an appropriate root of, $$j(\tau) = \frac{432}{1+f}\left(\frac{5+4f}{1 - f}\right)^3,\quad \text{where}\quad f = \frac{2\alpha+1}{2\sqrt{\alpha(1+\alpha)}}$$

P.S. Conjecture 2 is indebted to the answer by Noam Elkies, though the nature of $\tau$ which should provide the correct $\alpha(\tau)$ seems to have been left out.

Answer 1

(Updated.) Courtesy of Nemo's answer, we finally find a simple closed-form solution to the equation, $$\,_2F_1\Big(\tfrac13,\tfrac13;\tfrac56;- \alpha\Big)=\beta\tag1 $$ in algebraic numbers $\alpha, \beta$ analogous to this post. Let $\lambda=\frac{\eta\big(\tfrac{\tau+1}{3}\big)}{\eta(\tau)}$, then, $$\begin{aligned} \alpha &=\alpha(\tau) =\frac{(u-1)^2}{4u} =\frac1{4\sqrt{27}}\big(\lambda^3-\sqrt{27}\,\lambda^{-3}\big)^2\\[2.5mm] \beta &= \beta(\tau) =\frac{1+N}{432^{1/4}}\,\color{blue}{\frac{\sqrt{-3}}{1+\tau}}\, \frac{u^{1/3}}{(2u^2-2)^{1/3}}\frac{_2F_1\Big(\tfrac13,\tfrac23;1;\tfrac{u^2}{u^2-1}\Big)}{\pi^{-1}\,K(k_3)}\end{aligned}$$ where, $$u=\frac{\lambda^6}{\sqrt{27}},\quad\tau= \tfrac{1+N\sqrt{-3}}2$$ The formulas for the equality $(1)$ holds for real $N>1,$ but $\alpha(\tau)$ and $\beta(\tau)$ are algebraic numbers for integer $N>1$. Example: $$\alpha\big(\tfrac{1+7\sqrt{-3}}2\big) = 27,\quad\quad\beta\big(\tfrac{1+7\sqrt{-3}}2\big) = \tfrac47$$ Also, note that, $$\frac{\,_2F_1\Big(\tfrac13,\tfrac23;1;\,1-\tfrac{u^2}{u^2-1}\Big)}{\,_2F_1\Big(\tfrac13,\tfrac23;1;\tfrac{u^2}{u^2-1}\Big)}=\color{blue}{\frac{\sqrt{-3}}{1+\tau}}$$

---

(Old answer) It seems,

$$_2F_1\left(\frac16,\frac13;\frac12;\,\gamma^2\right)=\delta\tag1$$ $$_2F_1\left(\frac13,\frac13;\frac56;-\alpha\right)=\beta\tag2$$ are complementary. Let $N$ be any positive integer.

I. If $\color{brown}{\tau =N\sqrt{-3}}\,$ and $\gamma$ is an appropriate root of,

$$\color{blue}{j(\tau) = \frac{432}{1+\gamma}\left(\frac{5+4\gamma}{1 - \gamma}\right)^3}$$ or alternatively, $$\frac{108}{1-\gamma^2}=\left(\frac{\eta^6\big(\tfrac{\tau}{3}\big)}{\eta^6(\tau)} +27\frac{\eta^6(\tau)}{\eta^6\big(\tfrac{\tau}{3}\big)} \right)^2$$ then $\gamma^2$ and $\delta$ of $(1)$ are algebraic numbers. Example, if $\tau =2\sqrt{-3}$, then $\gamma^2=\frac{25}{27}$ and $\delta = \frac34\sqrt{3}$.

II. If $\color{brown}{\tau =\frac{1+N\sqrt{-3}}2}\,$ and $\alpha$ is an appropriate root of,

$$\color{blue}{j(\tau) = \frac{432}{1+f}\left(\frac{5+4f}{1 - f}\right)^3},\quad \text{where}\quad f = \frac{2\alpha+1}{2\sqrt{\alpha(1+\alpha)}}$$ or alternatively, $$432\,\alpha(1+\alpha)=\left(\frac{\eta^6\big(\tfrac{\tau+1}{3}\big)}{\eta^6(\tau)} -27\frac{\eta^6(\tau)}{\eta^6\big(\tfrac{\tau+1}{3}\big)} \right)^2$$ then $\alpha$ and $\beta$ of $(2)$ are also algebraic numbers. Example, if $\tau =\frac{1+7\sqrt{-3}}2$ then $\alpha = 27$ and $\beta = \frac47$.

Part 1, after some manipulation by the OP, can be derived a result in Zucker's and Joyce's, Special values of the hypergeometric series III. The fact that Part 2 shares tantalizing common forms suggest it may be amenable to a similar treatment.

Answer 2

The formula for $\beta={}_2F_1\Big(\tfrac{1}{3},\tfrac{1}{3};\tfrac{5}{6};-\alpha\Big)$ in terms of elliptic integrals is $$\large\begin{align} &{}_2F_1\Big(\tfrac{1}{3},\tfrac{1}{3};\tfrac{5}{6};\tfrac{1}{2}+i\tfrac{(2+2p-p^2) (1-2 p -2p^2) (1+4p+p^2)}{6 \sqrt{3} ~p(p+2) (2 p+1)(1-p^2)}\Big)\\&=\tfrac{\sqrt[3]{p(2+p)(1-p^2)}}{K(k_3)3^{1/4} (2 p+1)^{1/6}}\Big(e^{-\frac{\pi i}{6}}K\Big(\sqrt{\tfrac{p^3 (2+p)}{1+2 p}}\Big)+\tfrac{e^{\frac{\pi i}{6}}}{\sqrt{3}}K\Big(\sqrt{1-\tfrac{p^3 (2+p)}{1+2 p}}\Big)\Big) \end{align}\tag1$$ valid for $0<p<1$ (the proof is given at the end of this post). It can be continued analytically in the vicinity of this range. One can easily see from this formula how $\alpha$ and $\beta$ are parametrized in terms of $p$. However more work needs to be done to show that they are both algebraic when suitable parameter $\tau$ takes values $\tau=\frac{1+n\sqrt{-3}}{2}$, $~n\in\mathbb{N}$. To do this one needs parametrization in terms of eta quotients. Such parametrization is given in chapter 33, of Ramanujan's Notebooks, Part V (referred in the following as V).

Define (according to Lemma 5.5 in V) $$p(v)=-2\,\frac{\eta\big(\tfrac{v}2\big)\,\eta^3\big(6v\big)}{\eta\big(2v\big)\,\eta^3\big(\tfrac{3v}2\big)}\tag2$$

with $\large v=\frac{\tau}{\tau+1}.$ Then $$ \alpha(\tau)=-\tfrac{1}{2}-i\tfrac{(2+2p-p^2) (1-2 p -2p^2) (1+4p+p^2)}{6 \sqrt{3} ~p(p+2) (2 p+1)(1-p^2)} $$ $$ \beta(\tau)=\tfrac{\sqrt[3]{p(2+p)(1-p^2)}}{K(k_3)3^{1/4} (2 p+1)^{1/6}}\Big(e^{-\frac{\pi i}{6}}K\Big(\sqrt{\tfrac{p^3 (2+p)}{1+2 p}}\Big)+\tfrac{e^{\frac{\pi i}{6}}}{\sqrt{3}}K\Big(\sqrt{1-\tfrac{p^3 (2+p)}{1+2 p}}\Big)\Big) $$

Example: If $\tau=\frac{1+7\sqrt{-3}}2$, then $v=\frac{7i}{26 \sqrt{3}}+\frac{25}{26}$, and $\alpha=27$, $~\beta=4/7$.

Proof of such a connection between $\tau$ and $v$ is equivalent to verification of an eta function identity, as shown in the sequel (a simpler example of analogous verification can be found in this answer). First, using the trivial identity $\eta \left(\frac{v+1}{2}\right)=\frac{\zeta_{48} \eta (v)^3}{\eta \left(\frac{v}{2}\right) \eta (2 v)}$ and modular relations for eta functions one obtains $$ p(v)=\frac{\eta^3 (4x) \eta^3 (6x) \eta^6 (x)}{\eta (12x) \eta^2 \left(3x\right) \eta^9 (2x)},\quad x=(\tau+1)/6 $$ $$ \lambda=\frac{\eta\big(\tfrac{\tau+1}{3}\big)}{\eta(\tau)}=\zeta_{24}\frac{\eta\big(\tfrac{\tau+1}{3}\big)}{\eta(\tau+1)}=\zeta_{24}\frac{\eta\big(2x\big)}{\eta(6x)},\quad x=(\tau+1)/6. $$ Then $$ \alpha(\tau)=-\tfrac{1}{2}-i\tfrac{(2+2p-p^2) (1-2 p -2p^2) (1+4p+p^2)}{6 \sqrt{3} ~p(p+2) (2 p+1)(1-p^2)}=\tfrac1{4\sqrt{27}}\big(\lambda^3-\sqrt{27}\,\lambda^{-3}\big)^2 $$ becomes an eta function identity, which can be verified algorithmically.

It is known that if $z_1,z_2\in\mathfrak{H}$belong to an imaginary quadratic field then $\eta(z_1)/\eta(z_2)$ is algebraic. Since $\tau$ and also $v$ belong to $\mathbb{Q}[\sqrt{-3}]$ one obtains that $p(v)$ is algebraic. This proves that if $\tau=\frac{1+\sqrt{-3}}2$,$~n\in\mathbb{N}$ then $\alpha$ is algebraic. To show that $\beta$ is algebraic one needs to consider only the ratios $$ \frac{K\Big(\sqrt{\tfrac{p^3 (2+p)}{1+2 p}}\Big)}{K(k_3)},~~\frac{K\Big(\sqrt{1-\tfrac{p^3 (2+p)}{1+2 p}}\Big)}{K(k_3)}\tag3 $$ but since the elliptic integrals $K\Big(\sqrt{\tfrac{p^3 (2+p)}{1+2 p}}\Big)$, $K\Big(\sqrt{1-\tfrac{p^3 (2+p)}{1+2 p}}\Big)$ have complementary moduli algebraicity of one of the ratios would automatically imply algebraicity of the other ratio. More specifically there is the formula (provided by OP) $$ \frac{_2F_1\Big(\tfrac{1}{2},\tfrac{1}{2};1;1-\tfrac{p^3 (2+p)}{1+2 p}\Big)}{_2F_1\Big(\tfrac{1}{2},\tfrac{1}{2};1;\tfrac{p^3 (2+p)}{1+2 p}\Big)}=3(1-v)\sqrt{-1}=\frac{3\sqrt{-1}}{1+\tau}.\tag{4} $$

To prove it note that (5.1-5.14 in V) $$ p(v)+2=2\frac{\eta^2 (3 v) \eta \left({v}/{2}\right) \eta^3 (2 v)}{\eta^2 (v) \eta^3 \left({3 v}/{2}\right) \eta (6 v)} $$ $$ 2p(v)+1=\frac{\eta^2 (3 v) \eta^4 \left({v}/{2}\right) }{\eta^2 (v) \eta^4 \left({3 v}/{2}\right) }. $$ These formulas give $$ \frac{p^3 (2+p)}{1+2 p}=-\frac{16 \eta (6 v)^8}{\eta \left(\frac{3 v}{2}\right)^8}. $$ Further simplification by means of $\eta \left(\frac{v+1}{2}\right)=\frac{\zeta_{48} \eta (v)^3}{\eta \left(\frac{v}{2}\right) \eta (2 v)}$ and modular relation for eta function allows one to write $$ \frac{p^3 (2+p)}{1+2 p}=\left(\frac{\eta ((\tau+1)/6)^2 \eta (2(\tau+1)/3)}{\eta ((\tau+1)/3)^3}\right)^8.\tag{5} $$ From the theory of Jacobi elliptic functions it is known that $$ \omega=i\frac{K'}{K},~K=K(k),~K'=K(k'),~k'=\sqrt{1-k^2},~k'=\large \Big(\tfrac{\eta (2 \omega) \eta^2 (\omega/2)}{\eta^3 (\omega)}\Big)^4. $$ Comparing with (5) one gets $$ \frac{\tau+1}{3}=i\frac{K\Big(\sqrt{\tfrac{p^3 (2+p)}{1+2 p}}\Big)}{K\Big(\sqrt{1-\tfrac{p^3 (2+p)}{1+2 p}}\Big)} $$ equivalent to (4).

It is seen that $\frac{\tau+1}{3}$ is obtained from $\tau_0=n\sqrt{-3}$ by a shift $\tau_0\to\tau_0+1$, duplication, then another analogous shift and triplication. This means that the ratios (3) are algebraic.

---

Proof of equation (1). First step is to rewrite $\beta$ in terms of hypergeometric functions with the third parameter $1/2$ and $3/2$ according to eq. 2.11(3) from Erdelyi et. al. vol I

$${}_2F_1\Big(\tfrac{1}{3},\tfrac{1}{3};\tfrac{5}{6};\tfrac12+\tfrac{z}{2}\Big)=\tfrac{\sqrt{\pi } ~\Gamma \left(\frac{5}{6}\right)}{\Gamma \left(\frac{2}{3}\right)^2}{}_2F_1\Big(\tfrac{1}{6},\tfrac{1}{6};\tfrac{1}{2};z^2\Big)-z\tfrac{2\sqrt{\pi } ~\Gamma \left(\frac{5}{6}\right)}{\Gamma \left(\frac{1}{6}\right)^2}{}_2F_1\Big(\tfrac{2}{3},\tfrac{2}{3};\tfrac{3}{2};z^2\Big).\tag7$$

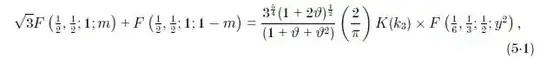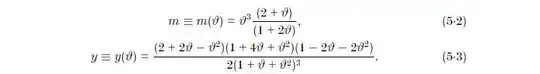Then the first hypergeometric on the lhs is converted to ${}_2F_1\Big(\tfrac{1}{6},\tfrac{1}{3};\tfrac{1}{2};\frac{z^2}{z^2-1}\Big)$ via Pfaff's transformation for which Zucker and Joyce in their third paper show that where The second hypergeometric function on the lhs of (7) is converted to ${}_2F_1\Big(\tfrac{2}{3},\tfrac{5}{6};\tfrac{3}{2};\frac{z^2}{z^2-1}\Big)$ by Pfaff's transformation, and subsequently to a sum of hypergeometric functions with the third parameter equal to $1$ with the help of eq. 2.11(9) from Erdelyi et. al. vol I $$ \sqrt{\tfrac{z^2}{z^2-1}}{}_2F_1\Big(\tfrac{2}{3},\tfrac{5}{6};\tfrac{3}{2};\tfrac{z^2}{z^2-1}\Big)={\tfrac{\Gamma \left(\frac{1}{6}\right) \Gamma \left(\frac{1}{3}\right)}{4z \sqrt{\pi }\Gamma \left(\tfrac{5}{6}\right)} \left(\, _2F_1\left(\tfrac{1}{3},\tfrac{2}{3};1;\tfrac{1}{2}-\tfrac{1}{2}\sqrt{\tfrac{z^2}{z^2-1}}\right)-\, _2F_1\left(\tfrac{1}{3},\tfrac{2}{3};1;\tfrac{1}{2}+\tfrac{1}{2}\sqrt{\tfrac{z^2}{z^2-1}}\right)\right)}. $$ Equation 5.17 in V enables one to write${}_2F_1\left(\tfrac{1}{3},\tfrac{2}{3};1;...\right)$ in terms of elliptic integrals. The required parametrization is $$ z=-i\frac{((2-p) p+2) (1-2 p (p+1)) (p (p+4)+1)}{3 \sqrt{3} p \left(2 p^4+5 p^3-5 p-2\right)}. $$ Combining all these formulas one eventually arrives at $$ \large\begin{align} \tfrac{2K(k_3)3^{1/4} (2 p+1)^{1/6}}{\pi \sqrt[3]{p(2+p)(1-p^2)}}{}_2F_1\Big(\tfrac{1}{3},\tfrac{1}{3};\tfrac{5}{6};\tfrac{1}{2}+i\tfrac{(2+2p-p^2) (1-2 p -2p^2) (1+4p+p^2)}{6 \sqrt{3} ~p(p+2) (2 p+1)(1-p^2)}\Big)\\=e^{-\frac{\pi i}{6}}{}_2F_1\Big(\tfrac{1}{2},\tfrac{1}{2};1;\tfrac{p^3 (2+p)}{1+2 p}\Big)+\tfrac{e^{\frac{\pi i}{6}}}{\sqrt{3}}{}_2F_1\Big(\tfrac{1}{2},\tfrac{1}{2};1;1-\tfrac{p^3 (2+p)}{1+2 p}\Big) \end{align}$$