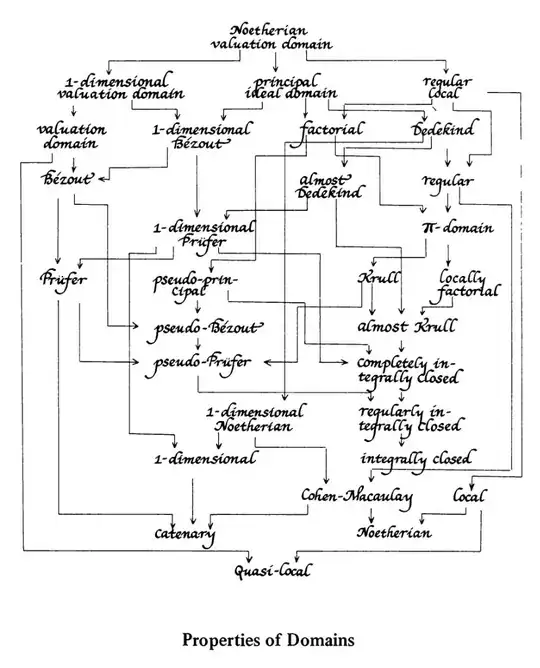
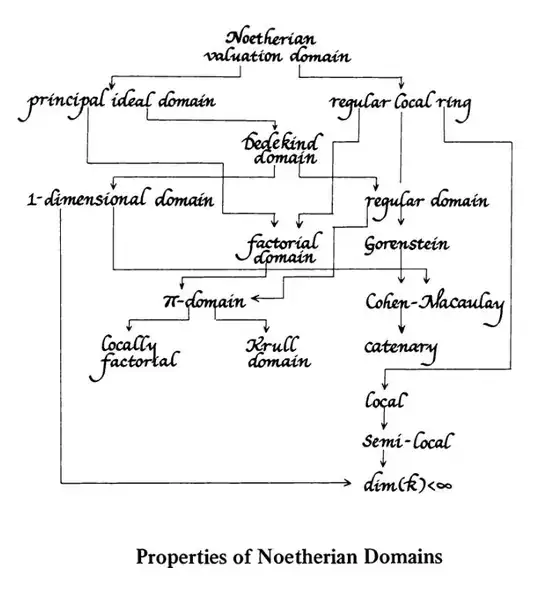
We say a ring is local iff its all nonunits form an (maximal) ideal.
But the integer set Z with the norm f(n)=|n| is a Euclidean domain and its all nonunits dont form an ideal; since 3, -2 are nonunit elements of Z but 3+(-2)=1 is a unit, thus nonunit elements doesnt form an additive subgroup, and thus an ideal.
Am i right? And then where the local domain is located? Like, we know that UFD > PID > ED > field. Is a local domain located between them? Or is it an independent concept?