5

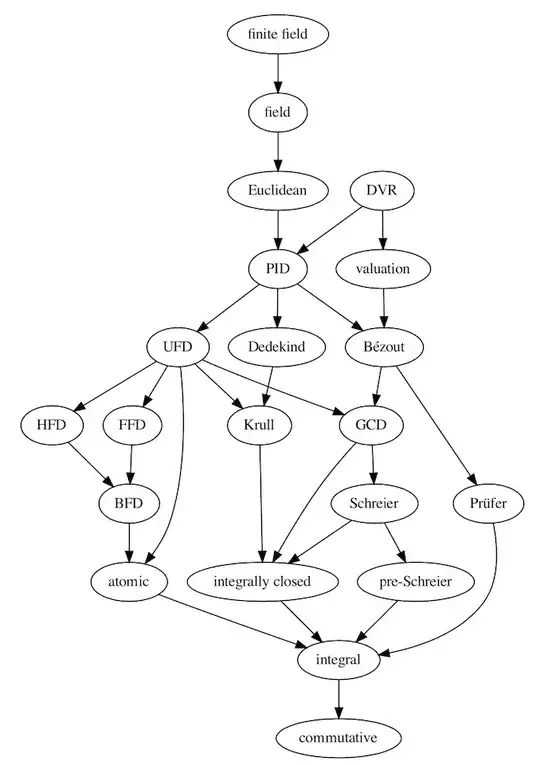
I made a directed graph in order to get a better understanding of the relationships between various types of commutative rings. Since I’m not very well versed in ring theory, I’m sure it can be improved. I’d like to know:

  • Are there any errors in the graph?
  • Are there any edges that could be added?
  • Are there any important types of commutative ring that could/should be added as nodes?

I’d be particularly interested in properties that split the edges that are currently unbranched along the main axis: between field and Euclidean domain, between Euclidean domain and principal ideal domain, and especially between integral domain and commutative ring.

I only want to show inclusion relationships (“Every principal ideal domain is a Bézout domain”), not theorems that require more than one of the properties as premises (“Every atomic Schreier domain is a unique factorization domain”) – though I intend to get to those as well, so feel free to mention particularly interesting or important ones.

The graph is only for commutative rings, so more general types like Noetherian rings are intentionally not included – but here, too, I’ll get to those eventually, so feel free to include important ones.

Here’s the graph (an arrow from $A$ to $B$ means “every $A$ is a $B$”; the nouns “ring” and “domain” are omitted):

$\hspace{60pt}$graph of relationships of types of commutative rings

The abbreviations mean: discrete valuation ring, principal ideal domain, unique factorization domain, greatest common divisor (domain), half-factorial domain, finite factorization domain, and bounded factorization domain.

Here’s the DOT code I used to generate the graph with the dot command in the Graphviz package:

digraph commutative_rings {
    "finite field" -> field -> Euclidean -> PID -> UFD -> GCD -> "integrally closed" -> integral -> commutative
    PID -> Bézout -> GCD
    Bézout -> Prüfer -> integral
    DVR -> PID -> Dedekind -> Krull -> "integrally closed"
    DVR -> valuation -> integral
    UFD -> Schreier -> "pre-Schreier" -> integral
    UFD -> atomic -> integral
    UFD -> Krull
    Schreier -> "integrally closed"
    UFD -> FFD -> BFD -> atomic
    UFD -> HFD -> BFD
}

P.S.: Here’s the modified graph with the two arrows suggested by Badam Baplan, valuation -> Bézout and GCD -> Schreier, which replace the arrows valuation -> integral and UFD -> Schreier:

modified graph with two new arrows suggested in a comment

joriki
  • 238,052
  • See this answer – Bill Dubuque May 03 '20 at 18:14
  • @Gone: Ha – very nice, thanks! – joriki May 03 '20 at 18:46
  • 1
    @Joriki at a glance, two arrows that should be added are valuation -> bezout and GCD -> schreier – Badam Baplan May 04 '20 at 21:47
  • @BadamBaplan: Thank you! Those arrows should then replace "valuation -> integral" and "UFD -> Schreier". – joriki May 04 '20 at 22:08
  • @joriki As for what to add, maybe you could elaborate on your interests a little bit more? Each of the classes in your graph is the lid to a juicy can of worms. In any case, you might consider adding a variety of chain conditions to your graph, e.g. Noetherian -> ACC on divisorial ideals (= Mori) -> ACC on principal ideals -> Archimedean. As with the graph linked to by Gone, other important properties having heavy interaction with the ones you've linked to are the properties of being $1$-dimensional (in the sense of Krull) and of being completely integrally closed. – Badam Baplan May 04 '20 at 22:11
  • @Joriki Adding any class between integral domains and commutative rings means adding considerations of zero divisors to your graph, and could cause it to explode. In my humble opinion, it doesn't make sense to construct such a graph without first settling on a fixed behavior of zero divisors, because the graph will inevitably either get out of control or lose cohesion. That said, most of these concepts have decent generalizations, e.g. to reduced rings, or at least reduced rings with restrictions on the minimal prime spectrum (like compactness); or perhaps to 'rings with few zero divisors.' – Badam Baplan May 04 '20 at 22:27

0 Answers0