Solve $e^x+x=1$

Question

This seems to have stumped even my TA, so I'm asking it here.

Given $e^x + x = 1$, solve for $x$.

I already know that the answer is zero, but have no idea how to get there.

Answer 1

Using the series expansion we have:

$$1+x+\frac{x^2}{2!}+ \dots + \frac{x^n}{n!}+\dots = 1-x$$

If $x$ is positive it is immediately obvious that there can be no equality.

If $x<0$ then the RHS is greater than 1 and $e^{x}<1$.

This is not strictly an "algebraic" solution, but with the term in $e^x$ we do not expect anything purely algebraic.

Answer 2

"Lambert W" is a hint for "algebraic solution".
The solution for $\mathrm{e}^x + x = 1$ is $1-\mathrm W(\mathrm{e})$,
to find ALL complex solutions, use all branches of the Lambert W ...

$$ \begin{align*} &\dots \\ 1 - \mathrm{W}_{-4}(\mathrm{e}) &= 3.159947300 + 23.47017395 i \\ 1 - \mathrm{W}_{-3}(\mathrm{e}) &= 2.849014724 + 17.17149358 i \\ 1 - \mathrm{W}_{-2}(\mathrm{e}) &= 2.393982241 + 10.86800606 i \\ 1 - \mathrm{W}_{-1}(\mathrm{e}) &= 1.532092122 + 4.597158013 i \\ 1 - \mathrm{W}_{0}(\mathrm{e}) &= 0.000000000 \\ 1 - \mathrm{W}_{1}(\mathrm{e}) &= 1.532092122 - 4.597158013 i \\ 1 - \mathrm{W}_{2}(\mathrm{e}) &= 2.393982241 - 10.86800606 i \\ 1 - \mathrm{W}_{3}(\mathrm{e}) &= 2.849014724 - 17.17149358 i \\ 1 - \mathrm{W}_{4}(\mathrm{e}) &= 3.159947300 - 23.47017395 i \\ 1 - \mathrm{W}_{5}(\mathrm{e}) &= 3.396557044 - 29.76478701 i \\ &\dots \end{align*} $$

explanation

$\mathrm{e}^x+x=1$
$\mathrm{e}^x=1-x$
$\mathrm{e} = (1-x)\mathrm{e}^{1-x}$
$\mathrm{W}(\mathrm{e}) = 1-x$
$x = 1-\mathrm W(\mathrm{e})$

Answer 3

You can see this very easily graphically. The equation is $$e^x=1-x$$ and the two sides of the equation are plotted here (from Wolfram Alpha):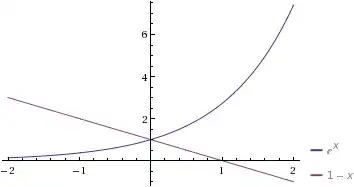

The intuition for a formal proof also follows directly from the picture (the functions are both monotonic but in opposite directions), if that's your aim.

Answer 4

Let $f(x) = e^x + x - 1$. Then, for any given $x$, $f(x) = 0$ if and only if $e^x + x = 1$.

You have already noticed that $f(0) = 1 + 0 - 1 = 0$, so it is a solution.

Now, we turn to calculus, not algebra. We have $f'(x) = e^x + 1$. Since $e^x > 0$ for all $x$, we know that $e^x + 1 > 0$ as well. In other words, $f'(x)$ is positive for all $x$ which tells us that $f(x)$ is an increasing function on the entire real line. Therefore, it could only possibly be 0 at one point, and you already found that point.

Now, if you haven't had calculus, you could still get the same basic idea. For example, you know $y = x$ is increasing. That is something you should know. Perhaps you have learned that $y = e^x$ is always increasing as well, because even in an algebra class, they would probably give you a bunch of properties of $y = e^x$ when they introduce it. Add these two functions together, and it's still increasing. Subtract 1, and the function is simply translated downward 1 unit, so it's still increasing everywhere. Again, the conclusion is the same.

Answer 5

Just to add weight to @Jonathan’s response: If $f$ and $g$ are an increasing and a decreasing function on $\mathbb{R}$ respectively, their graphs can cross at only one point. Inspection finds that point to be $(0,1)$, and you’re done.

Answer 6

This problem can be solved using domain arguments:

$e^{x} + x = 1$
$e^{x} = 1 - x$
$ln(e^{x}) = ln(1 - x)$
$x\cdot ln(e) = ln(1 - x)$

Which leads us to:
$x = ln(1-x)$

• $x$ cannot be larger than one, because then the expression $1-x$ will be negative violating the domain of a logarithmic function.
• $x$ cannot be a positive number between 0 and 1, because $ln(1-x)$ will be a negative value
• For the same reason, $x$ cannot be a number less than zero because $ln(1-x)$ will be a positive value

The only possible value for $x$ is 0.

Answer 7

Trial By Error is the only real solution.

Working with the graphical solution above, we can see that we can start with any random value for x, then recursively calling:-

for(x=i=0; i<5; x=1-((1-x+pow(M_E,x))/2.0), i++);

This takes the average value for both functions at the value of x, then re-inserting the new value for f(x) back into one of the original functions, to get a new value for x. Repeated 5 or so times to get a close estimate for the true value of x.

Answer 8

You can easily answer:

f(x)=e^x+x-1 The obvious solution is 0 and you can prove its the only one. By differentiating you get f'(x)=e^x+1 which is always positive.That means the f(x) function can only have one solution for zero because its monotonic.

Answer 9

Let's keep this one simple...

$$e^x+x=1$$

What here can give you $1+0$? Well, we know anything raised to 0 equals 1, and anything plus 0 equals it's self (at least in the reals) so... $e^0 + 0 = 1 + 0 = 1$... Just simple math intuition makes it easy to see that $e^x+x=1$ when $x=0$.

Answer 10

A semi-intuitive way to think about it: the right-hand side has no $e$, so whatever you plug into the $e^x$ has to kill the $e$. So it has to be $\ln a$ for some $a$. On the other hand, the right hand side has no $\ln$, so what you plug into the $x$ term must reduce to a non-$\ln$. If you try $\ln e^b$, you'll end up in a circle. If you think maybe things will cancel, you'll see that it wont work because you will always have a different number of "levels" of exponentials and logarithms. The only possibility is $\ln 1 = 0$, which quick inspection reveals that it works.

This is by no means a formal proof (at least as I've written it), but it provides the intuition to find the solution $x=0$ if you failed to notice it off the bat.

This also shows why the solution to something like $e^x + x = 2$ is not going to expressible in terms of functions like exponentials and natural logs.

And by the way, if you are also interested in complex solutions, all bets are off with this method, since $e^{x+2\pi i}=e^x$.