Forgive the possibly naive question, but I'm returning to a basic undergrad-level study of chaotic dynamical systems and can't quite seem to reconcile the notion that in order for a dynamical system to be considered chaotic, it must have positive global Lyapunov exponents. Such exponents, of course, drive the divergence of trajectories. However, topological transitivity implies that trajectories can get arbitrarily close as well over some finite time. It seems that positive Lyapunov exponents would disallow this mixing. Is there a point at which these positive exponents no longer describe the system, and the mixing behavior begins?
1 Answers
Is there a point at which these positive exponents no longer describe the system, and the mixing behavior begins?
Yes. The exponential divergence described by the Lyapunov exponents only affects trajectories whose separation is sufficiently close. Also, it only holds on average. For example, you can define the largest Lyapunov exponents as follows:
$$ λ_1 := \lim_{τ→∞} \; \lim_{|x(t)-y(t)|→0}\; \frac{1}{τ} \ln\left(\frac{|x(t+τ)-y(t+τ)|}{|x(t)-y(t)|}\right) $$
where $x$ and $y$ are two trajectories of your dynamics. Here, the limit $|x(t)-y(t)|→0$ ensures that you only consider the separation of infinitesimally close trajectories. (Also, see this question on Physics.)
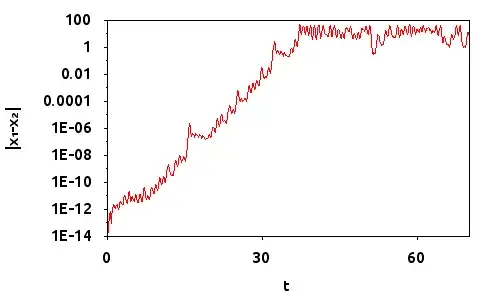
Once the separation of trajectories becomes too large, it is not exponentially growing but governed by the large-scale dynamics of the system. It then has some value that is of the order of magnitude of the size of the attractor (or invariant set) of your dynamics. E.g., here is the temporal evolution of two trajectories of the Lorenz system (attractor diameter $\approx 30$) starting off close by:
Now, you can see, that once the separation has reached the order of the magnitude of the attractor, it occasionally shrinks again (growing roughly exponentially afterwards). So the trajectories can come close to each other again. This happens along a direction corresponding to a negative Lyapunov exponent. This direction is orthogonal to the direction of largest separation which causes the positive Lyapunov exponents. This shrinking can be arbitrarily small and is the backbone of the topological transitivity.
-
So as a general heuristic for chaotic systems, do we typically only assume the largest exponent is positive, leaving the rest to be arbitrarily signed? – Joel Eliason Nov 30 '16 at 17:17
-
1No, what makes you think so? To have a chaotic dynamics you need at least one positive Lyapunov exponent (for the butterfly effect), one zero (for the time direction), and one negative (for topological transitivity). Possible further Lyapunov exponents are arbitrary, if you so wish. “Typically” they are negative. – Wrzlprmft Nov 30 '16 at 17:21
-
@Wrzlprmft You say that for "chaotic" behavior one needs at least one negative exponent. Take as prototype the map $z\mapsto z^2$ as a counterexample. On the typicality of nonzero exponents, since you make such a bold statement, perhaps you could expand on that (perhaps I say on advance that after working in the area for many years I have never seen such a statement, I mean rigorous...). – John B Nov 30 '16 at 21:29
-
@Jonas: That statement was specific for continuous-time systems (I should have said so). Regarding the zero Lyapunov exponent, see my answer to Joel’s follow-up question. Regarding the need for a negative Lyapunov exponent: You cannot have topological transitivity otherwise (see this answer). – Wrzlprmft Nov 30 '16 at 21:36
-
Actually there are "chaotic" flows (as you call them), having no negative exponent but still topologically transitive. – John B Dec 01 '16 at 01:33
-
@Jonas: I failed to find anything about this. Can you provide a reference? – Wrzlprmft Dec 01 '16 at 09:54
-
I would in case you provided the reference that I asked for. Sorry, I end it here. – John B Dec 01 '16 at 10:39
-
1@Jonas: I am not entirely sure, what you want referenced and thought your problem was my lack of restriction to continuous-time systems. Anyway, I added a reference to the other question on zero Lyapunov exponents. [to be continued] – Wrzlprmft Dec 01 '16 at 12:47
-
As for the negative Lyapunov exponent, take, e.g., Argyris et al – An Exploration of Dynamical Systems and Chaos (2015), p. 229: “Since a strange attractor occupies only a restricted part of the phase space, however, exponential growth is not possible in all directions; contractions and folding must of necessity occur. This behaviour is reflected in a negative Lyapunov exponent […]”. Also, if a dynamics has a positive and no negative Lyapunov exponents, its divergence would be positive and thus it would be neither dissipative nor conservative, but diverging and not be bounded anymore. – Wrzlprmft Dec 01 '16 at 12:47