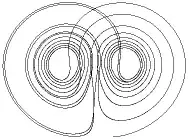
In the book of Chaosbook, at the beginning of chapter 6, it is given that
[...]if the attractor is strange, any two trajectories $x(t) = f^t(x_0)$ and $x(t)+\delta x(t) = f^t(x_0 + \delta x_0)$ that start out very close to each other separate exponentially with time [...]
However, we've all seen that the solutions stays in a surface similar to
, so any two solutions can't have an infinite divergence because any two of them stay in a surface similar to given above, and those surfaces will have a finite distance between them, so the solutions cannot diverge infinity apart, so am I taking the given explanation to literal, or am I just missing something because that kind of explanation for the Lyapunov exponent is, kind of, given in almost every chaos lecture, so I'm confused.