How can I define a bijection between sets $[-2,1)$ and $(3,5)$?

Question

I need to define a bijection between sets $[-2,1)$ and $(3,5)$. How can I do that?

Answer 1

I will write here how you should take $[3, 5) $ into $(3,5) $ and then you can compose @JeanMarie's map with mine to get the desired bijection.

Let us define the set $X = \{x_i = 3 + \frac1 {2^i} | i \in \Bbb N\} \cup \{3\} $ (let $x_0 = 3$) we know that $X $ has a countable infinite number of elements.

Let us define $\phi(x): [3, 5) \to (3,5) $ as follows:

$$\phi(x) = \begin{cases}\phi(x) = x, x \not\in X\\ \phi(x) = x_{i+1}, x \in X, x = x_i \end{cases} $$

$\phi $ is a bijection thus a composition with an appropriate linear map gives what you want.

Answer 2

Here is a function that maps open set $(-2,1)$ onto open set $(3,5)$ which is a different issue. When I realized that I was on a different problem, I wanted to erase this "answer". But the adequate answer by @RSerrao uses mine as a step. Therefore, I leave it...

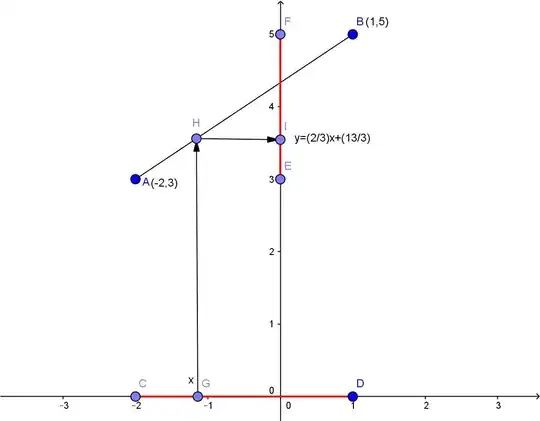
On the graphics below, have a look at the red intervals: one is $(-2,1)$ on $x$ axis, the other is $(3,5)$ on $y$ axis. The correspondence between them is an affine equation ($y=ax+b$), precisely:

$$\tag{1}y=(2/3)x+(13/3).$$

It can be explained by a kind of "mirror reflecting": the ray (vector $GH$) coming from $x \in (-2,1)$ is "reflected" into the straight line $HI$ with impact in a certain $y \in (3,5)$ that can be computed with formula $(1).$