1

I saw in several papers that there are at most three common tangents to two generic parabolas (of general form, i.e. not necessarily of then of $y = ax^2+bx+c$). But how can one prove it? using equations results in pretty tedious computations. In the case of two circles, the fact that the number of common tangents is max. 4 is pretty straight forward (see e.g. the second answer here), but I am really stuck with the case of two parabolas.

Can one, for example, look at the two parabolas in the projective plane $RP^2$ (now equivalent tocircles) and say that a "fourth" tangent of the two parabola is always the line at infinity, so one obtains as a result the other three tangents in the "real" part of the plane? Thank you!

Community
  • 1
user56531
  • 113
  • It can be proved that for two parabolas of equation $y=ax^2+bx+c$ there are in general two common tangents (never three).Why is it possible to draw three common tangents for general quadratic equation. Have you an example?. Are you sure of your reading in several papers as you have said.? – Piquito Nov 12 '16 at 00:14
  • @Piquito Two parabolas can have an additional exterior common tangent once you skew the axes e.g. this. – dxiv Nov 12 '16 at 01:55
  • I can't see a third tangent in this moment. I hope I shall do. Thank you very much. – Piquito Nov 12 '16 at 03:14

2 Answers2

4

One can use the point-line duality of the projective plane. For example, consider a generic conic of the form

$$(x,y,1)\cdot\begin{pmatrix}a&b&c\\b&d&e\\c&e&f\end{pmatrix} \cdot\begin{pmatrix}x\\y\\1\end{pmatrix}=0$$

then this matrix here describes the conic as a set of points $(x,y)$ or $[x:y:1]$ in homogeneous coordinates. The dual description would characterize the same curve as a set of tangent lines instead of points. The matrix for the dual conic in the non-degenerate case is the inverse of the primal matrix. This time you multiply with the vector $(a,b,c)$ from both sides, encoding the line $ax+by+c=0$.

(Including degenerate cases, multiplying the primal and the dual matrix must yield a multiple of the unit matrix. If the primal has at least rank 2 then the dual is its adjoint. If the primal is of rank 1 i.e. a double line then it doesn't contain enough information to completely define the dual.)

Replacing the roles of points and lines switches the roles of primal and dual description of a conic. So thinking about common tangents to two conics is the same as thinking about points of intersection of their duals. According to Bézout's theorem two conics will always have four points of intersection, algebraically speaking, although some of them may coincide and some of them may be complex. Which means two conics will have up to four real distinct common tangents.

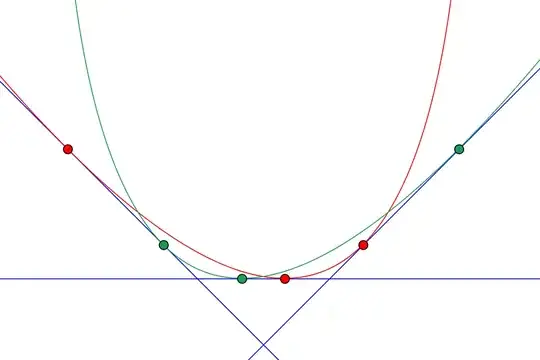
So far everything was for generic conics. Now parabolas are just those conics which have the line at infinity as a tangent, so as you rightly guessed in your question, once you know that there can be no more than four tangents for an arbitrary pair of conics, you know there can be no more than three finite tangents for a pair of parabolas.

Here is one example, constructed in Cinderella as a pair of conics defined by five lines each, with four of the lines in common, and one of these four located at infinity.

Example

MvG
  • 42,596
1

using a perspective transformation you can transform two parabolas into two ellipses. there will be at most 3 tangents + the 1 obtained from infinity.

cactus314
  • 24,438