12

Second Update: I see that some answers that reference my image are more closely answering my question. Here is a second image to clarify my point.

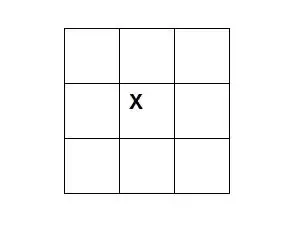
Take this image representing a checkerboard like configuration. If I asked you to move the X negative 1 space it would be impossible. You would have to make a guess as to which direction is negative. However, I can ask you to move the X 1 space/unit, since moving to any square from the center would satisfy moving 1 space/unit.

But wait! Once you complete moving the X 1 space/unit; I could now follow up and request you move negative 1 space, since you have now already travelled in one direction. Now you are able to negate the original request by 1 space/unit

Therefore negative doesn't exists until you have already begun moving in some direction/unit/space/time/apples.

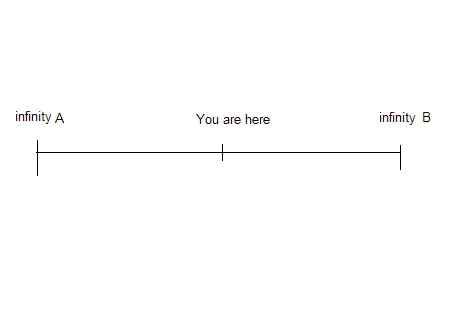
enter image description here

update enter image description here

Maybe this helps illustrate my point.

In this image there is a line, going either direction will take you to infinity (A or B), the number of spaces you move is always a positive number. If I moved 20 widgets closer to infinity A. or I moved 20 widgets closer to infinity B. So, negative numbers don't exist and are only positive numbers that are increasing in the opposite direction

Negative indicates the direction of travel on a line. the measure of movements will always be positive.

Does a negative number really exist? I can't have -1 apples. I can only imagine I had an apple when I really did not. Thus, in reality I would have -1 apple as compared to my imagination.

didn't know how to tag this

MVCylon
  • 271
  • Could you please explain what you mean with imaginary. What your wrote suggests that you mean it doesn't occur in nature rather than the complex meaning of imaginary. – Listing Feb 01 '11 at 19:36
  • 7
    @Doug: I think you can have minus one apple, e.g. if you owe me one. – Rudy the Reindeer Feb 01 '11 at 19:37
  • @Doug Chamberlain: "imaginary" is a term of art in mathematics. I think you mean to ask if negative numbers "really exist" or some such. – Arturo Magidin Feb 01 '11 at 19:37
  • 12
    @Doug: Does $1/2^{100}$ exist? You cannot have $1/2^{100}$ths of an apple: it would be less than a single atom... – Arturo Magidin Feb 01 '11 at 19:41
  • @Matt: I think you understand the most. But in your example, you would be minus one apple, not me. Think in terms of farenheit and kelvin. 0 degrees kelvin is like -273F. Therefore negative numbers indicate that in the original equation there was an over estimation of the amount available. therefore negative numbers are not (a number) they are simply a [positive integer?] placeholder representing how wrong the original math was. – MVCylon Feb 01 '11 at 19:45
  • 7
    @Doug Chamberlain: So, $1/2$ also does not exist; if I give you half an apple, it just demonstrates that you were wrong to consider the previous item as a single whole, when you should have considered it as two of the thing I'm giving you now? Of course, this is all just semantic games. Positive integers don't "exist" either, because you cannot show me "1", you can only show me any number of "one of ", not "one" by itself. Are you asking whether negative integers can be instantiated? – Arturo Magidin Feb 01 '11 at 19:50
  • As an aside: negative numbers were at one time refered to as "imaginary"; in his Geometry, Descartes talks about solving certain problems by using square roots, and then says what to do when the quantity inside the radical is "imaginary", meaning negative. – Arturo Magidin Feb 01 '11 at 19:52
  • 3
    @Doug: You might find some of the discussion in this previous question relevant: Do infinity and zero really exist? –  Feb 01 '11 at 19:53
  • @ArturoMagidin: But isn't it also true that a fraction is not a number? That's why they are called fractions? – MVCylon Feb 01 '11 at 20:06
  • See related: [Do complex numbers really exist?] (http://math.stackexchange.com/questions/154/do-complex-numbers-really-exist). – Jason Feb 01 '11 at 20:07
  • @Doug: Fractions are a kind of number, just like negatives and reals are kinds of number. Some fractions are not so-called whole numbers. (Others are: e.g., $\frac{6}{3}$). But we're back to the semantic games. Are you arguing that one cannot have "one half"? And I still don't see any instance of "1", just of "1 something". P.S. No matter how many steps you take in whatever direction, you did not get "closer to infinity". – Arturo Magidin Feb 01 '11 at 20:17
  • 10
    @Doug: So... does any number "actually exist"? I'm still waiting to see "1". – Arturo Magidin Feb 01 '11 at 20:19
  • 2
    @Doug: You need to supply a (rigorous) mathematical definition of "really exists". Otherwise your question is not mathematical. – Bill Dubuque Feb 01 '11 at 20:37
  • @BillDubuque: It is possible to have a question and not know how to ask it. My last word; I'm asking if Negation is simply the reversal of the direction on a number line and not an actual number. negative literally means (switch direction) positive becomes negative and negative becomes positive. therefore how can it be a number? AND negative is an operator meaning an indicator of how to manipulate numbers – MVCylon Feb 01 '11 at 21:26
  • 2
    @Doug: What does "actual number" mean? A number is just a mathematical object. It is ideal and it obeys certain axioms. That is all. – Asaf Karagila Feb 01 '11 at 22:08
  • @Doug you are confusing the definitions of displacement/position (which are vector quantities) and number – Vicfred Feb 02 '11 at 14:35
  • 27
    I find it humorous that this question currently has a score of -1. –  Mar 24 '11 at 07:53
  • Of course they exist! In fact, infinite number of them exist! – Aleksei Averchenko Jul 01 '11 at 08:51
  • 2
    Define "exists" please. Oh, and if you want this question to actually get resolved, make sure you don't have a philosophically contentious definition of "existence". – Doug Spoonwood Jul 01 '11 at 15:34
  • 5
    Does the vote total of this question really exist? – Qiaochu Yuan Jul 01 '11 at 15:53
  • In some sense, "negative numbers" only exist in the presence of an orientation. Orientations are chosen usually somewhat arbitrarily. For example, if "+1" means "increase by one", then "-1" means "decrease by one". You could be perverse and assign these meanings oppositely, and that would still "make sense". – David Wheeler Jul 21 '12 at 09:18
  • I think the question is a bit related to this http://physics.stackexchange.com/questions/63517/esotic-quantities-and-visualization – MphLee May 13 '13 at 14:22
  • do these kinds of questions really exist ? – Abr001am Jun 17 '15 at 09:50
  • I can't wait to the number 1337 walking down the street – user541686 Jun 18 '15 at 10:09

9 Answers9

32

Asking whether a negative number "really exists" is not really a meaningful question, to my mind. A number (of any kind) is an abstract mathematical idea, and it's not really clear how to talk about whether ideas "exist". Does justice really exist?

However, what we can say is that there are situations in the real world for which the idea of a negative number gives a useful description or model: any situation where something is removed or decreased.

Nate Eldredge
  • 97,710
13

Where the philosophy of negative numbers "existing" is concerned, I think Nate Eldredge answered the question very nicely. However, let me post a separate answer (really an extended comment) to address the diagram.

I think there's some confusion regarding the distinction between position and distance.

If we want to talk about position on the diagram that you've drawn, then one natural way of doing so is introducing some sort of coordinate system. Let's start by labelling "You are here" as 0. Going to the right, we can introduce 1, 2, 3,... (in whatever your favorite unit is). Going to the left, we have a couple of options:

  • We could perhaps label going to the left as 1, 2, 3,... -- but then we have to specify what side of "here" we're on: left or right. In other words, one's position on the line would have to be specified as "x units left" or "x units right."

  • An easier approach, then, might be to label the left side as -1, -2, -3....

The point is, though, that these two approaches are equivalent: Here $-x$ means "x units left."

But if we want to talk about distance -- that is, how far we are from "here," independent of our direction -- then, yes, our distance will always be positive.

Mathematically, this can be represented by taking the absolute value of the position. This makes sense since the absolute value of a number is often defined as "distance from zero," thereby forgetting about the distinction between left and right.

Jesse Madnick
  • 31,524
  • That is my point. negative is an indicator of direction like "east" or "west", but the distance moved is always a "number" or unit. Picture a chess board. Any direction you move your piece is always positive. You can only consider it a negative when it is relative to the direction you were travelling in the previous moment. You must say I first moved 1 space then I moved 1 space in the negative direction. – MVCylon Feb 02 '11 at 13:53
  • 2
    Sure, that's a fine intuition about how positive and negative work, but it's important to realize that it's just an intuition. That is, intuitions alone are not mathematically precise. – Jesse Madnick Feb 02 '11 at 14:41
  • And if you would like to say that a "number" has to be positive... well, certainly no one can stop you from doing so: after all, you can define anything to be whatever you like, really. But you should be aware that the widely-held convention is to refer to objects like -1, -2, etc as negative numbers. And again, the question about whether such objects exist was answered in other posts. – Jesse Madnick Feb 02 '11 at 14:45
  • Reading your second update, I'm starting to think that your question boils down to asking: "Is my intuition about positive and negative valid?" Again, I would say that yes, it is a valid intuition. – Jesse Madnick Feb 02 '11 at 14:52
  • @JesseMadnick: You seem to have understood my non-math ramblings, and answered in a way I could comprehend. Someone else may have given a righter ;) answer. Perhaps, I just couldn't understand it. – MVCylon Feb 02 '11 at 15:16
  • Negative isn't always an indicator of direction or distance. The integers under addition form a group, and every integer has its "negative" or inverse. Or equivalently, "-" can get thought of as a unary function on the integers. – Doug Spoonwood Jul 01 '11 at 15:38
  • @MVCylon: If you don't know which direction is negative, how can you know which direction is positive? –  Feb 08 '13 at 06:06
6

I think this is rather a philosophical than a mathematical question. The question whether numbers exist is almost as old as mathematics itself.

When I think about this I always have to smile and think about something like the image from René Magritte: enter image description here

It says in french "this is not a pipe". The question you ask is very simillar. Of course we encounter numbers in the nature, but are they already there or did we invent them?

Maybe this link could also be interesting:

http://queuea9.wordpress.com/category/philosophy/

Listing
  • 13,937
4

The term 'imaginary' in mathematics is usually reserved for a technical concept involving $\sqrt{-1}$. Because it is easy to confuse with the normal everday English usage of 'existing only in the imagination', mathematician's prefer to use 'complex number' instead.

If you are wondering whether a negative number 'exists only in the imagination', then I agree it is hard to be very literal and count a negative number of apples.

But numbers have many uses (and so follow many different rules). Think of money: suppose you have 5 dollars in your hand but you owe someone 7 dollars. Then in on sense/use of numbers you really have a usable amount of -2 dollars.

The difficulty with negative numbers is that, well, the positive numbers are just so obviously represented by objects, but negative numbers are not. But really, both kinds, positive and negative, are in your imagination. You don't have 5 in your hands, you have 5 dollars in your hand and the 5 is really how your imagination will deal with the situation.

Mitch
  • 8,591
  • thanks for the explanation; Math is not my primary area of expertise. See my comment above in the OP. – MVCylon Feb 01 '11 at 19:50
  • 1
    You said "mathematician's prefer to use 'complex number' instead". That's not right. Properly, for a mathematician, an imaginary number is a real multiple of $i$, and a complex number is a sum of a real and an imaginary one. Both terms (with their different meanings) are regularly used in the mathematical literature. In particular, it is standard to talk about the imaginary part of a complex number. – Martin Argerami Mar 31 '12 at 14:24
1

$-1$ is an integer. It is not imaginary. It is a complex number with zero imaginary part (i.e. $-1 = -1 + 0i$).

NebulousReveal
  • 13,935
1

In your image

number line

you have a line. Suppose we want to label the point on this line for the purpose of describing things that we can measure (i.e. number of apples, temperature of sun or moon, charge on a particle, weight of a car, etc). The line is not very useful in and of itself for this purpose because it has no point of reference. The ends will not do for such a purpose as they are at infinity. We therefore define a reference point, a datum, or a landmark on the line (you call it "you are here") called zero. We then adopt conventions stating that a certain distance from that datum is one 'unit' which we call 1. We use this point as a abstract way to refer to the number of a given set of objects. It could be one apple, one car, one planet, one atom; we use the same label to refer to one unit of anything. We then define other labels (i.e. 2,3,4,...) as multiples of this unit to count. Some things that we want to label are not discrete objects, but can be divided continuously such as distance (i.e. distance from home to work is 13.77 miles). Here we are assuming that we are always on the same side of our datum '0'. There are other quantities that we measure and wish to label that can be increased arbitrarily but also decreased arbitrarily such as electric charge, a force, a moment, a voltage, a DC current, etc. In these cases, we not only want to signify how far we are from our datum, but we also want to know which side of the datum we are on. We use negative numbers to signify that our quantity is the same in magnitude but opposite in direction of what we decide to call positive (an arbitrary choice by the way).

Tpofofn
  • 4,771
1

Think about it. Does a positive number really exist?

Just like negative numbers, complex numbers, positive numbers have a status that is no different. And you can ask the same question for other mathematical objects, sets, groups, etc. (And depending on what you mean by "exist").

Think about complex numbers. At first glance, they look like non-sense. I mean how can $\sqrt{-1}$ exist? But when I read complex analysis, I realized what a beauty I was missing. My heart was more than ever, ready to accept the existence of complex numbers. "It gave us a new way to model this world", and "new way to derive meaning from complexity and confusion", and thats what most mathematical objects do in the end, even though they may take abstraction to the highest level.

If you look at it more closely, the problem is not with "numbers", the problem is with the word "exist". My answer to your doubt will be "Cogito ergo sum" (I think therefore I am).

Peace :)

Roupam Ghosh
  • 1,913
  • Mathematics is 'a' representation which helps us to derived and understand the algorithms and structures of nature/reality or whatever anyone calls it isn't it? – Buddhika Chaturanga Feb 09 '19 at 09:35
1

I don't pretend to know the answer, but a lot of smart people (e.g. Gödel) think the question is meaningful and even have positions on the matter. See

http://en.wikipedia.org/wiki/Philosophy_of_mathematics#Contemporary_schools_of_thought

Incidentally, I think most philosophers (and mathematicians for that matter) would distinguish numbers from their application to physical concepts of magnitude, direction, distance, quantity, etc. So just because you find the application of a particular number system (like integers) to a particular physical concept (like directed distance) unnatural, that doesn't directly bear on the existence question. It could be that your mathematical model is a poor fit for the physical phenomenon. In the particular example you give, however, the integers are a proven good fit, as they wrap magnitude and direction into a single number. The magnitude is always positive, yes, but the number is the combination of the magnitude and the sign.

0

Doug, one cannot move in the opposite direction ($-1$) with relation to anything until one has chosen a direction, i.e. a basis.

No numbers exist other than in theory -- negative, positive, imaginary, or otherwise. Can you point to $3$ in the real world? Not to an example of $3$ (like 3 rocks) but $3$ itself?

Willard van Orman Quine had an interesting way of defining what $3$ itself is: $3 \equiv \text{ the equivalence class of all sets with cardinality } 3$. Can you use that kind of reasoning to come up with a definition of $-3$ ?

isomorphismes
  • 4,542