Asymptotic analysis of the integral $\int_0^1 \exp\{n (t+\log t) + \sqrt{n} wt\}\,dt$

Question

The integral I'm trying to study is

$$ F(n) = \int_0^1 \exp\left\{n(t+\log t)+\sqrt{n}wt\right\}\,dt, \tag{1} $$

where $w$ is a fixed complex number with $\Re(w) < 0$ and $\Im(w) > 0$. As I'll indicate below, I "expect" an asymptotic expression of the form

$$ F(n) \sim A e^{n+\sqrt{n}w} n^{-1}. $$

My first attempt at estimating $(1)$ was to try to address the problem of the oscillatory integrand. I set out to mimic the method of steepest descent and deform the contour of integration so that the imaginary part of the argument $f(n,t) = n(t+\log t)+\sqrt{n}wt$ was constant.

The image below shows where $\Re(f(n,t)) = \text{const.}$ (thick lines), where $\Im(f(n,t)) = \text{const.}$ (thin lines), and the interval $(0,1)$ (red line). The parameter $n$ has been fixed at $10$.

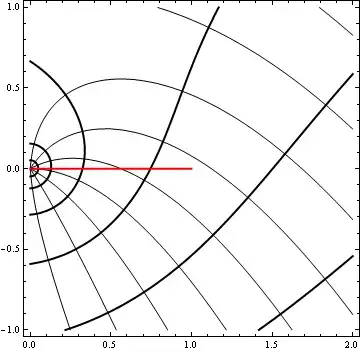
By Cauchy's theorem I can deform the contour $(0,1)$ to the contour $C_n$, on which

$$ \Im(f(n,t)) = \sqrt{n}\Im(w), $$

shown in red below.

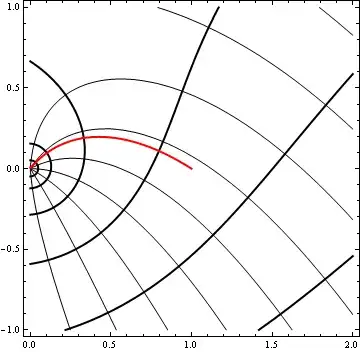
Thus I have

$$ \begin{align} F(n) &= \int_{C_n} \exp\left\{n(t+\log t)+\sqrt{n}wt\right\}\,dt \\ &= \int_{C_n} \exp\left\{\Re\left(n(t+\log t)+\sqrt{n}wt\right) + \sqrt{n}\Im(w)\right\}\,dt \\ &= e^{\sqrt{n}\Im(w)} \int_{C_n} \exp\left\{n(\Re(t)+\log |t|)+\sqrt{n}\Re(wt)\right\}\,dt, \end{align} $$

so that at least now I'm dealing with a real integral. However, I don't know where to go from here. It's clear that $C_n \to (0,1)$ as $n \to \infty$, so I think the last integral above could be asymptotic to

$$ \int_0^1 \exp\left\{n(\Re(t)+\log |t|)+\sqrt{n}\Re(wt)\right\}\,dt = \int_0^1 \exp\left\{n(t+\log t)+\sqrt{n}\Re(w)t\right\}\,dt, \tag{2} $$

but I don't know how to bound the "error"

$$ \int_{E_n} \exp\left\{n(\Re(t)+\log |t|)+\sqrt{n}\Re(wt)\right\}\,dt, $$

where $E_n$ is the closed loop $C_n \cup -(0,1)$, shown below.

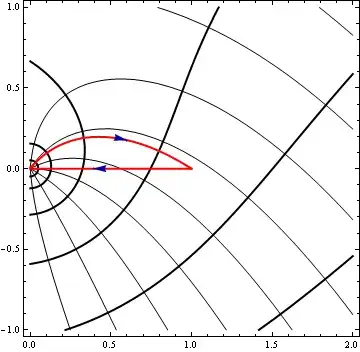
If this error is sufficiently small, I could see if I could apply the general ideas of the standard Laplace method to the real integral $(2)$, though it's not of the usual form. My guess would be that

$$ \int_0^1 \exp\left\{n(t+\log t)+\sqrt{n}\Re(w)t\right\}\,dt \sim A e^{n+\sqrt{n}\Re(w)} n^{-1} $$

since the largest contribution to the integral comes from a neighborhood of $t=1$.

Any help would be greatly appreciated.

Answer 1

The only condition we impose on $w$ is that we can find a constant $C$ such that $\operatorname{Re} w \geq C$. If we take $n > C^2+1$ (so that the quantity $n + \sqrt{n} \operatorname{Re} w$ is bounded below by a positive constant) then we ensure that all estimates herein hold uniformly with respect to $w$.

We begin by changing variables $t = 1-s$ to get

\begin{align*} &\int_0^1 \exp\left\{n(t+\log t)+\sqrt{n}wt\right\} dt \\ &\qquad = e^{n+w\sqrt{n}} \int_0^1 \exp\left\{n[\log(1-s)-s]-\sqrt{n}ws\right\}ds \tag{$*$} \end{align*}

and note that for $s<1$ we have \begin{align*} n[\log(1-s)-s]-\sqrt{n}ws &= -\left(2n+\sqrt{n}w\right)s - n \sum_{k=2}^{\infty} \frac{s^k}{k}. \end{align*}

The largest contribution of the integrand now comes from a neighborhood of $s=0$ of width $O\left(1/\sqrt{n}\right)$. Indeed, the contribution from the rest of the interval is exponentially small:

\begin{align*} &\left|\int_{1/\sqrt{n}}^1 \exp\left\{n[\log(1-s)-s]-\sqrt{n}ws\right\}ds\right| \\ &\qquad \leq \int_{1/\sqrt{n}}^1 \exp\left\{n[\log(1-s)-s]-\sqrt{n}\operatorname{Re}(w)s\right\}ds \\ &\qquad \leq \left(1-\frac{1}{\sqrt{n}}\right)\exp\left\{n\left[\log\left(1-\frac{1}{\sqrt{n}}\right)-\frac{1}{\sqrt{n}}\right]-\operatorname{Re} w\right\} \\ &\qquad \leq \exp\left\{-2\sqrt{n} - \operatorname{Re} w\right\}, \tag{1} \end{align*}

where the second inequality follows from our assumption on the size of $n$ and the third from $\log(1-x) \leq x$. Over the remaining interval $0 \leq s \leq 1/\sqrt{n}$ we have

$$ \exp\left\{-n \sum_{k=2}^{\infty} \frac{s^k}{k}\right\} = 1 + O\left(n s^2\right) $$

by expanding the exponential as a power series, so our goal is now to estimate

\begin{align*} &\int_0^{1/\sqrt{n}} \exp\left\{n[\log(1-s)-s]-\sqrt{n}ws\right\}ds \\ &\qquad = \int_0^{1/\sqrt{n}} e^{-\left(2n+\sqrt{n}w\right)s}\,ds + O\left(n\int_0^{1/\sqrt{n}} e^{-\left(2n+\sqrt{n}w\right)s} s^2\,ds\right). \tag{2} \end{align*}

The line $y=ex$ is tangent to the curve $y=e^x$ at $x=1$, so from convexity of the exponential we have $e^x \geq ex > 2x$ for all $x \geq 0$. Thus $e^x-x^2$ is increasing and hence $x^2 < e^x \leq e^{nx}$ for all $x \geq 0$ and $n \geq 1$. We therefore have

\begin{align*} \left|\int_{1/\sqrt{n}}^\infty e^{-\left(2n+\sqrt{n}w\right)s} s^2 \,ds\right| &\leq \int_{1/\sqrt{n}}^\infty e^{-\left(2n+\sqrt{n}\operatorname{Re} w\right)s} s^2 \,ds \\ &< \int_{1/\sqrt{n}}^\infty e^{-\left(n+\sqrt{n}\operatorname{Re} w\right)s} \,ds \\ &= \frac{e^{-\sqrt{n}-\operatorname{Re} w}}{n+\sqrt{n}\operatorname{Re} w} \\ &= O\left(n^{-1}e^{-\sqrt{n}-\operatorname{Re} w}\right), \end{align*}

whence

\begin{align*} \int_{0}^{1/\sqrt{n}} e^{-\left(2n+\sqrt{n}w\right)s} s^2 \,ds &= \int_0^\infty e^{-\left(2n+\sqrt{n}w\right)s} s^2 \,ds + O\left(n^{-1}e^{-\sqrt{n}-\operatorname{Re} w}\right) \\ &= 2 \left(2n+\sqrt{n}w\right)^{-3} + O\left(n^{-1}e^{-\sqrt{n}-\operatorname{Re} w}\right). \tag{3} \end{align*}

Similarly,

\begin{align*} \int_0^{1/\sqrt{n}} e^{-\left(2n+\sqrt{n}w\right)s} \,ds &= \int_0^\infty e^{-\left(2n+\sqrt{n}w\right)s} \,ds + O\left(e^{-2\sqrt{n}-\operatorname{Re} w}\right) \\ &= \left(2n+\sqrt{n}w\right)^{-1} + O\left(e^{-2\sqrt{n}-\operatorname{Re} w}\right). \tag{4} \end{align*}

Combining $(1)$, $(2)$, $(3)$, and $(4)$ we find that

\begin{align*} &\int_0^1 \exp\left\{n[\log(1-s)-s]-\sqrt{n}ws\right\}ds \\ &\qquad = \left(2n+\sqrt{n}w\right)^{-1} + O\left(n\left(2n+\sqrt{n}w\right)^{-3}\right) + O\left(e^{-\sqrt{n}-\operatorname{Re} w}\right) \tag{$**$} \end{align*}

uniformly for $\operatorname{Re} w > C$ and $n > C^2+1$. In terms of the original integral $(*)$ we have shown that

$$ \int_0^1 \exp\left\{n(t+\log t)+\sqrt{n}wt\right\}dt \sim \frac{e^{n+\sqrt{n}w}}{2n+\sqrt{n}w} $$ as $n \to \infty$.

It is interesting to note that $(**)$ also yields the correct asymptotic as $\operatorname{Re} w \to \infty$.

Answer 2

Note that $$\exp(n(t+ \log t) + \sqrt{n} w t) = \exp((n+\sqrt{n}w)t ) \exp(n \log t) = t^n \exp((n+\sqrt{n}w)t)$$ Hence, since the integrand is entire, we can make the substitution $y = (n+\sqrt{n}w)t$ to get the lower incomplete $\gamma$ function $$\int_0^1 t^n \exp((n+\sqrt{n}w)t) dt = \dfrac{\gamma(n+1,n+w \sqrt{n})}{(n+w \sqrt{n})^{n+1} } = \dfrac{\Gamma(n+1)}{e^{n+w \sqrt{n}}} \sum_{k=0}^{\infty} \dfrac{(n+w \sqrt{n})^{k}}{\Gamma(n+k+2)}$$ Once you have this, working out the asymptotic should not be hard using Stirling formula and similar tools.