I am trying to integrate this: $$\int_0^\infty\frac{ 1}{x^2} \, \mathrm d x$$ I was trying to convert it into a complex integral. But did not know how to proceed.
My original question is : $$\int_0^\infty\frac{1-\cos x}{x^2}\, \mathrm dx$$.
Can someone give me a hint on how to proceed.
Thanks in advance.
Consider the contour integral \begin{align} \int_C f(z)\ dz=\int_{C}\frac{1-e^{iz}}{z^2}\ dz \end{align} where $C=L_1+C_R +L_2 +C_\epsilon$ is given by
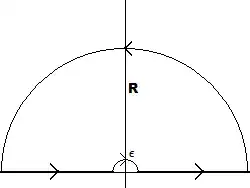
It's not hard to see that $f(z)$ has a pole of order 2 at $z=0$ and analytic everywhere else. Hence by Cauchy's theorem, we have that \begin{align} \int_{L_1} \frac{1-e^{iz}}{z^2}\ dz + \int_{C_R}\frac{1-e^{iz}}{z^2}\ dz+ \int_{L_2}\frac{1-e^{iz}}{z^2}\ dz+\int_{C_\epsilon}\frac{1-e^{iz}}{z^2}\ dz = 0. \end{align} Let us simplify each integral. Observe \begin{align} \int_{L_1} \frac{1-e^{iz}}{z^2}\ dz = \int^R_{\epsilon} \frac{1- e^{ix}}{x^2}\ dx = \int^R_{\epsilon}\frac{1-\cos x}{x^2}\ dx - i\int^R_\epsilon \frac{\sin x}{x^2}\ dx \end{align} and \begin{align} \int_{L_2} \frac{1-e^{iz}}{z^2}\ dz =&\ \int^{-\epsilon}_{-R} \frac{1-e^{ix}}{x^2}\ dx = \int^{-\epsilon}_{-R}\frac{1-\cos x}{x^2}\ dx - i\int^{-\epsilon}_{-R} \frac{\sin x}{x^2}\ dx \\ =&\ \int^R_\epsilon \frac{1-\cos x}{x^2}\ dx + i\int^{R}_{\epsilon} \frac{\sin x}{x^2}\ dx \end{align} which means \begin{align} \int_{L_1} \frac{1-e^{iz}}{z^2}\ dz+\int_{L_2} \frac{1-e^{iz}}{z^2}\ dz= 2\int^R_{\epsilon} \frac{1-\cos x}{x^2}\ dx. \end{align} Next, by Jordan's lemma we see that \begin{align} \left|\int_{C_R}\frac{1-e^{iz}}{z^2}\ dz\right|\rightarrow 0 \end{align} as $R \rightarrow \infty$. Lastly, by the fractional residue theorem, we have that \begin{align} \lim_{\epsilon\rightarrow 0}\int_{C_\epsilon} \frac{1-e^{iz}}{z^2}\ dz= -\pi i \operatorname{Res}_{z=0} f(z) = -\pi . \end{align} Thus, it follows \begin{align} \int^\infty_0 \frac{1-\cos x}{x^2}\ dx = \frac{\pi}{2}. \end{align}
