I am trying to solve this question.
$$\int_0^\infty \frac{1-\cos(x)}{x^2}dx$$
As this function $f(x) =\frac{1-\cos(x)}{x^2} $ has a removable singularity at $z = 0$.Is it possible to solve this using complex integration.If not why ?
Other solutions to this problem are in : Find the principal value of $\int_{-\infty}^{\infty}\frac{1-\cos x}{x^2}\,\mathrm dx$
Thanks
Integrate $$f(z)=\frac{1-e^{iz}}{z^2}$$ over the contour $\gamma$ shown below.
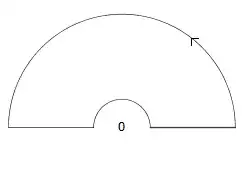
where the circles are centered at $0$, line segments lie on the real line, the small circle has radius $r$, the large circle has radius $R$. We consider the limiting case when $R\to+\infty, r\to 0$.
Contribution of the small circle is $$ -\pi i\,\text{Res}(f,0)=-\pi i(-i)=-\pi $$ On the large circle we have $$ |f(z)|=O(R^{-2})\implies \Big{|}\int_{\text{large circle}}f(z)dz\Big{|}=O(R^{-1})\implies\lim_{R\to\infty}\int_{\text{large circle}}f(z)\,dz=0 $$ Contribution of the real line is $$ \text{p.v. }\int_{-\infty}^\infty\frac{1-e^{ix}}{x^2}\,dx $$ By residue theorem $$ \text{p.v. }\int_{-\infty}^\infty\frac{1-e^{ix}}{x^2}\,dx-\pi=0 $$ Equating real parts we see $$ \text{p.v. }\int_{-\infty}^\infty\frac{1-\cos x}{x^2}\,dx=\pi $$ Noting that the integrand is an even function we see $$ \text{p.v. }\int_{0}^\infty\frac{1-\cos x}{x^2}\,dx=\frac{\pi}{2} $$
