4

Consider three geometric transformations.

1st: The geometric "proof" that hypotenuse of a right triangle is equal to the sum of squares of the other sides. The link is here.

2nd: The famous "pi=4" "proof" by geometric transformation

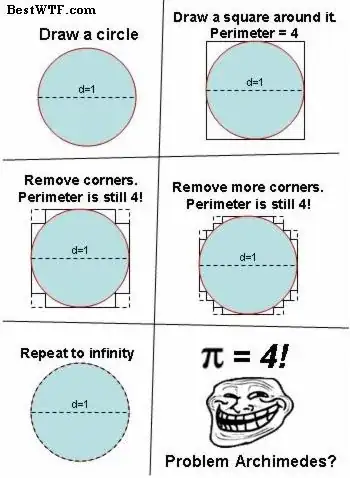
3rd: Archimedes's method of calculation of pi

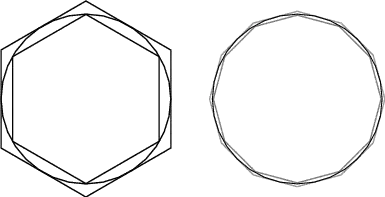
What is inherently different in these transformations that 1st 2nd yield wrong results while the 3rd doesn't? Is there any heuristic which could hint us when the transformation is valid for calculation of the limit? I have read the discussion on mathstackexchange about pi=4, but still I couldn't get that intuition. There was an interesting argument about the divergence of the derivatives of those two curves. But I still don't understand if it is a satisfactory condition to prove that Archimedes construction was a valid one.

If possible, please give 2 two explanations from intuitional and strictly mathematical point of view.

Glorfindel
  • 3,955
guser
  • 581

2 Answers2

1

The key point is the lower semicontinuity (and in general the non-continuity) of the perimeter when you approximate (in some sense to be made more precise) a given region $R$ with some regions $R_n$ (for example polygons). So you can only say in general that $$ \textrm{Per}(R)\leq\liminf_n \textrm{Per}(R_n). $$ Nothing more. If, for some reasons, you know a priori that, for any $n$, $\textrm{Per}(R)\geq \textrm{Per}(R_n) $, then you can conclude $$ \textrm{Per}(R)= \textrm{Per}(R_n). $$ This is the case of the approximation of the circle with the inscribed polygons: you postulates that the chord is always less than the arc, i.e. the straight line is the minimum lenght curve, so $\textrm{Per}(R)\geq \textrm{Per}(R_n) \;\forall n$.

Of course this further property does't apply in your approximation with the external polygons and, in fact, for this approximation $$ \pi= \textrm{Per}(R)<\liminf_n \textrm{Per}(R_n)=\liminf_n 4=4. $$

guestDiego
  • 4,006
  • your external perimeter is always and always and always equal to 4, never less and never more. – hamam_Abdallah Oct 12 '16 at 15:36
  • Waht's the point of this comment? – guestDiego Oct 12 '16 at 15:47
  • Of course this further property does't apply in your approximation with the external polygons and, in fact, for this approximation π=Per(R)<lim infnPer(Rn)=lim infn4=4.

    @guestDiego You can also approximate pi with circumscribed polygons. Naturally enough, they also converge to pi. So there is nothing connected with the fact of the polygons being circumscribed or inscribed to a curve or in this case a circle.

     – guser Oct 12 '16 at 16:21
  • @guser. Instead it is! The approximation with the external polygons works for circumscribed polygons but not for the polygons you showed in your construction. And the reason is exactly the one I explained. – guestDiego Oct 12 '16 at 16:25
0

From the first figure pi<4. In each step n, the area of the polygon, a(n), is the same and equals 4. Hence lim a(n) = 4, as n tends to infinity and we still have pi < 4.

frank trevor
  • 1