The way I would treat this is using
$$f(z) = \frac{1}{z}
\exp((-1/2)\mathrm{LogA}(z+1))
\exp((-1/2)\mathrm{LogB}(z-1))$$
with $\mathrm{LogA}$ the branch with argument from $-\pi$ to $\pi$ and
$\mathrm{LogB}$ the branch with argument from $0$ to $2\pi$. The first
logarithm has branch cut $(-\infty, -1)$ on the negative real axis and
the second one from $[1,\infty)$ on the positive real axis.
We use the contour integral
$$ \int_\Gamma f(z) dz$$
where $\Gamma$ consists of six components namely a circle $\Gamma_0$
$1+\epsilon e^{i\theta}$ centered at one with $0\lt\theta\lt 2\pi$
traversed clockwise, a line segment $\Gamma_1$ just above the cut from
$\mathrm{LogB}$ connecting to $\Gamma_0$ and continuing up to the
point $R$ on the positive real axis, a quarter circle $\Gamma_2$
parameterized by $Re^{i\theta}$ with $0\lt\theta\lt \pi/2$ traversed
counterclockwise and connecting $\Gamma_1$ to the point $iR$ on the
imaginary axis, a line segment $\Gamma_3$ connecting $iR$ to $-iR$ on
the imaginary axis, a quarter circle $\Gamma_4$ parameterized by
$Re^{i\theta}$ with $-\pi/2\lt \theta\lt 0$ traversed counterclockwise
and finally a line segment $\Gamma_5$ just below the cut of
$\mathrm{LogB}$ connecting $\Gamma_4$ to $\Gamma_0.$
Call the target integral $J$ i.e.
$$J = \int_1^\infty \frac{1}{x\sqrt{x^2-1}} dx.$$
Now along $\Gamma_1$ we get
$$f(z) = \frac{1}{x}
\exp((-1/2)\log(x+1))
\exp((-1/2)\log(x-1))
= \frac{1}{x\sqrt{x^2-1}}$$
while on $\Gamma_5$ we obtain
$$f(z) = \frac{1}{x}
\exp((-1/2)\log(x+1))
\exp((-1/2)\log(x-1)+(-1/2)2\pi i)
\\ = \exp(-\pi i))\frac{1}{x\sqrt{x^2-1}}
= -\frac{1}{x\sqrt{x^2-1}}.$$
Therefore the contribution from $\Gamma_1$ and $\Gamma_5$ in the limit
is $2J.$ We then obtain
$$2J = 2\pi i \times \frac{1}{2} \mathrm{Res}_{z=0} f(z)$$
if we can show that the remaining contributions vanish/cancel. Note
however that
$$\mathrm{Res}_{z=0} f(z) =
\exp((-1/2)\mathrm{LogA}(1))\exp((-1/2)\mathrm{LogB}(-1))
\\ = \exp((-1/2)\pi i) = -i$$
so that this yields
$$\bbox[5px,border:2px solid #00A000]{
J = \pi i\times \frac{1}{2} \times (-i)
= \frac{\pi}{2}.}$$
which is the desired result. (Here we have used the property of
$\Gamma_3$ being a line segment passing through the pole at $z=0$ and
hence picking up half the residue.)
To conclude we must examine the remaining segments of the
contour. To apply the ML bound to $\Gamma_0$ we observe that
$$\left|\frac{1}{1+\epsilon e^{i\theta}}
\exp((-1/2)\mathrm{LogA}(2+\epsilon e^{i\theta}))
\exp((-1/2)\mathrm{LogB}(\epsilon e^{i\theta}))\right|
\\ \le \frac{1}{1-\epsilon}
\exp((-1/2)\log(2-\epsilon))
\exp((-1/2)\log(\epsilon))$$
where we have used the fact that the imaginary term produced by the
two logarithms being exponentiated has modulus one. ML now yields
$$2\pi\epsilon \times \frac{1}{1-\epsilon}
\frac{1}{\sqrt{2-\epsilon}} \frac{1}{\sqrt\epsilon}
\rightarrow 0 \quad\text{as}\quad \epsilon\rightarrow 0.$$
For $\Gamma_2$ and $\Gamma_4$ we get (these are alike and we discuss
$\Gamma_2$)
$$\left|\frac{1}{1+R e^{i\theta}}
\exp((-1/2)\mathrm{LogA}(1 + R e^{i\theta}))
\exp((-1/2)\mathrm{LogB}(-1 + R e^{i\theta}))\right|
\\ \le \frac{1}{R-1}
\exp((-1/2)\log(R-1))
\exp((-1/2)\log(R-1))$$
so that ML yields
$$\frac{1}{4}\times 2\pi R\times
\frac{1}{R-1} \frac{1}{\sqrt{R-1}} \frac{1}{\sqrt{R-1}}
\\ = \frac{1}{4}\times 2\pi R\times
\frac{1}{(R-1)^2}
\rightarrow 0 \quad\text{as}\quad R\rightarrow \infty.$$
We now show that the contribution from $\Gamma_3$ is zero where we
will traverse clockwise to simplify the notation. We have
$$f(it) =
\frac{1}{it}
\exp((-1/2)\mathrm{LogA}(it+1))
\exp((-1/2)\mathrm{LogB}(it-1))
\\ = \frac{1}{it}
\exp((-1/2)\log\sqrt{t^2+1}+(-1/2)i\mathrm{ArgA}(it+1))\\ \times
\exp((-1/2)\log\sqrt{t^2+1}+(-1/2)i\mathrm{ArgB}(it-1)).$$
Observe however that when $\mathrm{ArgA}(it+1)=\theta$ with
$-\pi/2\lt\theta\lt\pi/2$ we have $\mathrm{ArgB}(it-1)=\pi - \theta$
so that this simplifies to
$$f(it) =
\frac{1}{it} \frac{1}{\sqrt{t^2+1}}
\exp((-1/2)i(\theta+\pi-\theta))
= -\frac{1}{t\sqrt{t^2+1}}.$$
Supposing we make a semicircular indentation of radius $\epsilon$
around the singularity at $t=0$ we get for the upper segment
parameterized by $z=it$
$$\int_\epsilon^R f(it) i\; dt.$$
We get for the lower segment
$$\int_{-R}^{-\epsilon} f(it) i\; dt
= -\int_R^\epsilon f(-iu) i\; du
= \int_\epsilon^R f(-iu) i\; du
= -\int_\epsilon^R f(iu) i\; du.$$
The two segments cancel for a net contribution of zero. We have
examined all six constituents of the closed contour $\Gamma$ and this
concludes the argument showing that $J=\frac{\pi}{2}.$
Addendum, Oct 8 2016. In order to justify the segment
$\Gamma_3$ passing through the pole at $z_0 = 0$ we observe that a
function $f(z)$ with a simple pole at $z_0$ has the form
$$f(z) = F'(z) + \frac{1}{z-z_0} \mathrm{Res}_{z=z_0} f(z)$$
with $F(z)$ analytic in a neighborhood of $z_0.$ Now by making a small
semicircular indentation $\Gamma_3'$ that is parameterized by $z=z_0 +
\epsilon e^{i\theta}$ with $\theta$ ranging from $\pi/2$ to $-\pi/2$
so as to capture the inner angle we get for the integral of $f(z)$
along the semicircle with $F(z)$ analytic
$$F(z_0-i\epsilon) - F(z_0+i\epsilon)
+ \mathrm{Res}_{z=z_0} f(z) \times
\int_{\Gamma_3'} \frac{1}{z-z_0} dz
\\ = F(z_0-i\epsilon) - F(z_0+i\epsilon)
+ \mathrm{Res}_{z=z_0} f(z) \times
\int_{\pi/2}^{-\pi/2} \frac{1}{\epsilon\exp(i\theta)}
i\epsilon\exp(i\theta) \; d\theta
\\ = F(z_0-i\epsilon) - F(z_0+i\epsilon)
+ i \mathrm{Res}_{z=z_0} f(z) \times
[\theta]_{\pi/2}^{-\pi/2}.$$
This becomes
$$-\pi i \mathrm{Res}_{z=z_0} f(z)$$
as $\epsilon\rightarrow 0.$ We thus obtain
$$2J - \pi i \times (-i) = 2\pi i \times 0$$
or $2J - \pi = 0$ as before. This material is from this MSE
link and this
German complex variables
PDF.
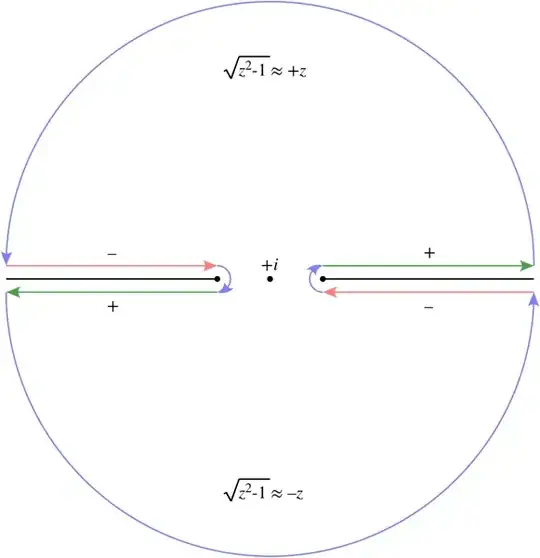
Addendum, Oct 9 2016. The excellent answer by @robjohn states
the contributions on the two horizontal segments above and below the
left branch cut without proof. It may be interesting to see how these
are computed. Starting again from
$$f(z) = \frac{1}{z}
\exp((-1/2)\mathrm{LogA}(z+1))
\exp((-1/2)\mathrm{LogB}(z-1))$$
we take a point on the negative real axis $x < -1$ and get from above
$$\frac{1}{x}
\exp((-1/2)\log(-x-1)+(-1/2)i\pi)
\exp((-1/2)\log(-x+1)+(-1/2)i\pi)
\\ = \frac{1}{x\sqrt{(-x)^2-1}} \exp(-i\pi)
= - \frac{1}{x\sqrt{x^2-1}}.$$
The contribution is thus
$$- \int_{-\infty}^{-1} \frac{1}{x\sqrt{x^2-1}} dx
= - \int_{\infty}^{1} \frac{1}{(-u)\sqrt{u^2-1}} (-1) du
\\ = - \int_{\infty}^{1} \frac{1}{u\sqrt{u^2-1}} du
= \int_1^{\infty} \frac{1}{u\sqrt{u^2-1}} du = J.$$
On the other hand we get from below
$$\frac{1}{x}
\exp((-1/2)\log(-x-1)+(-1/2)(-i\pi))
\exp((-1/2)\log(-x+1)+(-1/2)i\pi)
\\ = \frac{1}{x\sqrt{x^2-1}}.$$
The contribution is now
$$\int_{-1}^{-\infty} \frac{1}{x\sqrt{x^2-1}} dx
= \int_1^{\infty} \frac{1}{(-u)\sqrt{u^2-1}} (-1) du
\\ = \int_1^{\infty} \frac{1}{u\sqrt{u^2-1}} du = J.$$