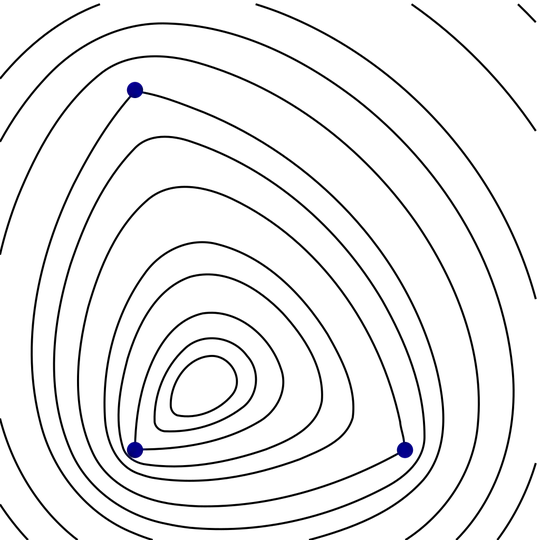
I have a problem similar to that of finding the geometric median. Suppose I have $n$ fixed points $x_1,x_2,\dots,x_n$; what is the set of points that have the same total distance $\ell$ to these fixed points?
Is there any theory relating to this problem? Is there any chance that these points have some relationship with the geometric median?