How can I calculate a point's coordinates given distances from three other known points?

Question

I have a trilateration-related problem that I'm unsure how to solve mathematically. I can see a solution is possible through geometry, but I'm unsure how to solve the resulting equations.

Given three 2D points, find where to put a new point on the same plane. You know the exact distances from the new point to each existing point.

By drawing a picture, it is clear that this is attainable:

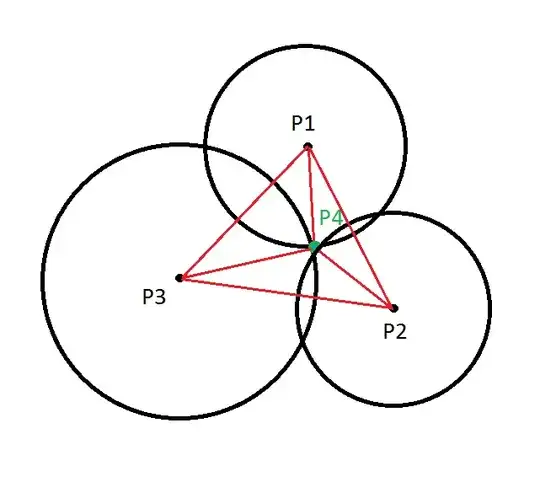
In this image, $P_1,P_2,P_3$ are the known points, and $P_4$ is the point we want to find coordinates for. The red lines denote known distances.

Given only two points, we can find 2 candidate positions (where the circles intersect), while the third given point limits us to our solution.

Using the properties of circles, I have come up with 3 equations and 2 unknowns. Let $P_i=[x_i,y_i]^T$ and $r_i=|P_i-P_4|$ for $i\in\{1,2,3,4\}$. Then my set of equations, expanded, is $$r_1^2 = (x_4 - x_1)^2 + (y_4 - y_1)^2\\ r_2^2 = (x_4 - x_2)^2 + (y_4 - y_2)^2\\ r_3^2 = (x_4 - x_3)^2 + (y_4 - y_3)^2$$ How can I calculate $x_4$ and $y_4$?

---

I FOUND THE ANSWER I WAS LOOKING FOR

(I'd answer my own question, but since it's closed as a duplicate all I can do is post it here)

So I was hoping to find a way to express this as a linear least-squares ($Ax=b$) type problem. I mentioned that in the comments, but not in this OP. Regardless, the link from @dxiv in the comments below helped me get to this solutions. Also worth mentioning, the question this is a duplicate of reaches the same conclusion (as it obviously should). It just stops short of the $Ax=b$ form.

In short, the approach is to combine the 3 quadratic equations to get 2 linear ones.

Given

$$\text{(1) } r_1^2 = (x_4 - x_1)^2 + (y_4 - y_1)^2\\ \text{(2) }r_2^2 = (x_4 - x_2)^2 + (y_4 - y_2)^2\\ \text{(3) }r_3^2 = (x_4 - x_3)^2 + (y_4 - y_3)^2$$

we first expand each to

$r_i^2 = \hat{x}^2 + \hat{y}^2 - 2\hat{x}x_i - 2\hat{y}y_i + x_i^2 + y_i^2$

Then we subtract (2) from (1) and (3) from (1):

$$\text{(1)-(2) }2\hat{x}(x_2 - x_1) + 2\hat{y}(y_2 - y_1) + (x_1^2 - x_2^2) + (y_1^2 - y_2^2) - (r_1^2 - r_2^2) = 0\\ \text{(1)-(3) }2\hat{x}(x_3 - x_1) + 2\hat{y}(y_3 - y_1) + (x_1^2 - x_3^2) + (y_1^2 - y_3^2) - (r_1^2 - r_3^2) = 0$$

This is now able to be expressed as an least-squares problem, particularly as an $Ax=0$ (i.e. nullspace) problem if the distances $r_i$ are precise.

$\left[ \begin{matrix} 2(x_2 - x_1) & 2(y_2 - y_1) & (x_1^2 - x_2^2) + (y_1^2 - y_2^2) - (r_1^2 - r_2^2) \\ 2(x_3 - x_1) & 2(y_3 - y_1) & (x_1^2 - x_3^2) + (y_1^2 - y_3^2) - (r_1^2 - r_3^2) \end{matrix} \right] \left[ \begin{matrix} \hat{x} \\ \hat{y} \\ 1 \\ \end{matrix} \right] \left[ \begin{matrix} 0 \\ 0 \end{matrix} \right] $

Thus, in short, the solution for $\left[ \begin{matrix} \hat{x} \\ \hat{y} \end{matrix} \right]$ is found in the nullspace of the $A$ matrix.

If the distances $r_i$ have some uncertainty, this can be expressed as a linear least-squares minimization problem which is easily solvable using SVD.

Answer 1

Simplify, by changing to an easier coordinate system. When you find the result, do the inverse.

Let's rotate and translate (but not scale) the coordinate system so that $\vec{P}_1$ is at origin, and $\vec{P}_2$ is at $(r_{12}, 0)$ on the positive $x$ axis. The $y$ axis is perpendicular to it, increasing towards $\vec{P}_3$. The basis vectors are $$\begin{cases} \hat{e}_x = \frac{\vec{P}_2 - \vec{P}_1}{\lvert \vec{P}_2 - \vec{P}_1 \rvert} \\ \hat{e}_y = \frac{\vec{P}_3 - \vec{P}_1 - \hat{e}_x \left( (\vec{P}_3 - \vec{P}_1) . \hat{e}_x \right)}{\lvert \vec{P}_3 - \vec{P}_1 - \hat{e}_x \left( (\vec{P}_3 - \vec{P}_1) . \hat{e}_x \right) \rvert} \end{cases}$$ In these new coordinates, $$\begin{array}{rl} \vec{p}_1 =& (0, 0) \\ \vec{p}_2 =& (r_{12}, 0) \\ \vec{p}_3 =& (a, b) \\ \end{array}$$ where $a = (\vec{P}_3 - \vec{P}_1) . \vec{e}_x$ and $b = (\vec{P}_3 - \vec{P}_1) . \vec{e}_y \ge 0$.

If we use $\vec{p}_4 = (x, y)$ in these new coordinates, then the equations regarding the first two points are $$\begin{cases} x^2 + y^2 = r_1^2 \\ (r_{12} - x)^2 + y^2 = r_2^2 \end{cases}$$ Subtracting the latter from the former we get $$2 r_{12} x - r_{12}^2 = r_1^2 - r_2^2$$ which we can trivially solve for $x$: $$x = \frac{r_1^2 + r_{12}^2 - r_2^2}{2 r_{12}}$$ We can then solve for $y$, too (by solving for $y$ in the first equation in the pair), $$y = \pm \sqrt{ r_1^2 - x^2 }$$

The equation for the third point is $$(x - a)^2 + (y - b)^2 = r_3^2$$ and only the positive or the negative $y$ should fulfill it; indeed, $$y = b \pm \sqrt{r_3^2 - (x - a)^2}$$

When you have solved both $x$ and $y$ in these new coordinates, you can finally convert back to original coordinates: $$\vec{P}_4 = \vec{P}_1 + x \hat{e}_x + y \hat{e}_y$$

---

The system of three equations in two dimensions is actually overdetermined. That is, there may not be any solutions at all.

When the coordinates and distances contain noise, or you do computations with finite precision, the order in which you label the three points affects the results. A common mitigation tactic is to calculate the result in three possible combinations -- there are six possible combinations, but the order of the two first points really only affects rounding --, and use e.g. their centroid (coordinate average) as the result.

More properly, the system of equations can be solved using linear least squares.

However, in real applications, calculating the three points is typically much faster, and their distances (compared to the known distances) gives a very practically useful indication of the magnitude of noise or errors in the system.