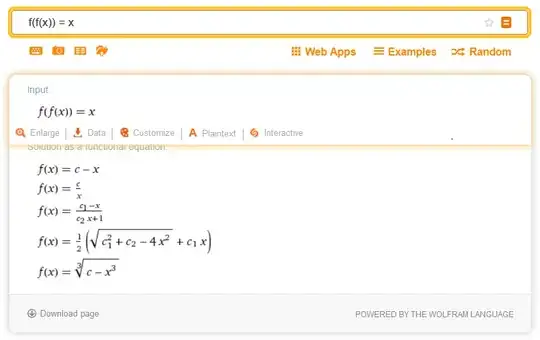
Seems simple enough, but I have no idea how one would get all solutions to this. Wolfram Alpha gives $5$ answers, the first $2$ of which I could get myself, but the following $3$ completely defeat me.
Asked
Active
Viewed 5,200 times
12
-
3Such functions are known as involutions. In general, given an invertible function $g$, $f(x)=g^{-1}(-g(x))$ is an involution. – Workaholic Sep 22 '16 at 12:58
-
7This is simple indeed, only on an entirely different level. There is a great deal of solutions, not just mere 5 or 50. – Ivan Neretin Sep 22 '16 at 13:02
-
I think it would suffice to prove that $f(x)=x$ is the only solution of this functional equation. – Student Sep 22 '16 at 13:08
-
1At first I thought the question was how to solve $f(f(x) = x$ for $x$. Obviously that depends on $f$! Now I understand the question is how to solve $f \circ f = \text{Id}$ for $f$, which is definitely nontrivial. – Matthew Leingang Sep 22 '16 at 13:09
-
@ShreyAryan But it isn't. Depending on the domain of $f$ there are other solutions (and $\sqrt[3]{1-x^3}$ is a solution on $\mathbb{R}$). – Winther Sep 22 '16 at 13:09
-
1interesting question (+1) – tired Sep 22 '16 at 13:10
-
2notice also that solutions one and two are special cases of the solution 3 – tired Sep 22 '16 at 13:12
-
Involution. Related MSE questions: (1), (2) – Winther Sep 22 '16 at 13:17
-
Yeah, I thought this must have been asked before. So in fact, this question is a duplicate, and so is my answer (both halves of it). There were many before it. Wonder why the "Related" column didn't put them forth. – Ivan Neretin Sep 22 '16 at 14:07
-
Even $\frac{x}{\sqrt{x^2-1}}$ satisfies it. – Aman Sharma Apr 23 '17 at 11:32
1 Answers
10
If you want a continuous solution:
- Draw a graph of $y=x$ (this is an auxiliary construction, you will erase it later).
- Starting at any point on the graph, draw a freehand graph of a decreasing function.
- Draw the reflection of that graph with respect to the line $y=x$.
- Erase the line $y=x$. What remains is the graph of your function.
If you want just any solution:
- Select two arbitrary non-intersecting equinumerous sets $A,B\in\mathbb R$. (They can be empty, or finite, or countably infinite, or uncountably infinite; that doesn't matter.)
- Select any bijection $A\leftrightarrow B$.
- For any $x\in A$, let $f(x)$ be the image of $x$ in $B$ under that bijection, and vice versa.
- For any $x\in\mathbb R\setminus(A\cup B)$, let $f(x)=x$.
Ivan Neretin
- 12,835