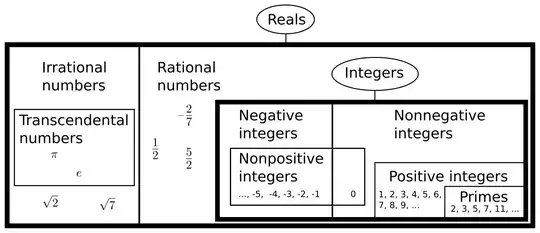
I am working on a simple proof involving rational and irrational numbers. Is it safe to assume that if a number is not rational, it is irrational, and that if a number is not irrational, it is rational?
Example: Let $P(x)=\text{x is rational}$ and $Q(x)=\text{x is irrational}$.
Then is it true that $\forall x\ P(x)\text{ xor }Q(x)$?
A rational number is defined as a number that can be expressed as the ratio of two integers, i.e. $\frac{p}{q}$, where $q\ne0$. An irrational number is a real number that cannot be expressed as a ratio. So, yes a real number is either rational or irrational, but not both.
An irrational number is a number that is not rational.
Thus a non-irrational number is not (a number that is not rational), thus it is rational.
In set notation irrational numbers are $\mathbb{R}\setminus\mathbb{Q}$, so non-irrational numbers are $\mathbb{R}\setminus(\mathbb{R}\setminus\mathbb{Q})=\mathbb{Q}$.
The real numbers are composed of the rational numbers and the irrational numbers so yes if a number is not one, it is the other.
See Dominik's answer:
Are there real numbers that are neither rational nor irrational?
There he provided this excellent picture:
