$P^{-1}A^{-1}B P$ diagonal implies $P^\top A P$ and $P^\top B P$ diagonal?

Question

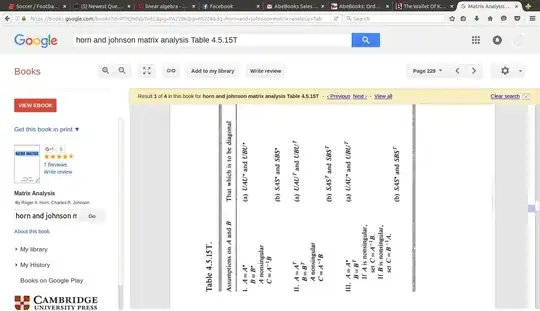
Consider two symmetric positive-definite real matrices $A,B$. $A$ is hence invertible. Denote by $P$ the matrix of the column-eigenvectors of $A^{-1}B$ such that $P^{-1}A^{-1}BP=D$ where $D$ is a diagonal matrix of the eigenvalues of $A^{-1}B$.

$A^{-1}B$ is symmetric and real, hence can be diagonalized in an orthogonal basis, but this does not mean that $P$ is necessarily orthogonal.

It seems that $P^\top A P$ and $P^\top B P$ are diagonal. Is it always true, and if so, why?

What is not clear to me is the meaning of $P^\top$ instead of $P^{-1}$. I wonder whether this is related to a change of basis (for example, the change of basis of the bilinear forms defined by $A$ and $B$).

---

Edit I think this is true only if $A^{-1}B$ has distinct eigenvalues. Indeed, let $v_i$ denote an eigenvector of $A^{-1}B$ for $\lambda_i>0$ (because it is PD), then $A^{-1}B v_i=\lambda_i v_i$ or $Bv_i=\lambda A v_i$ so that $v_j^\top B v_i=\lambda_i v_j^\top A v_i$ and similarly $v_i^\top B v_j=\lambda_j v_i^\top A v_j$. Substracting one equality to the other: $$ (\lambda_j-\lambda_i)v_i^\top A v_j=(\lambda_j-\lambda_i)v_i^\top \dfrac{1}{\lambda_j} B v_j.$$ Hence, if $\lambda_i\neq\lambda_j$, necessarily $v_i^\top A v_j=v_i^\top B v_j=0$ or $V^\top A V$ and $V^\top B V$ are diagonal, where $V$ is a matrix of columns the $v_i$. Does it seem correct?

Answer 1

As indicated in another answer, this is generally false. What is true, however, that you can choose $P$ such that $P^{-1}A^{-1}BP=D$, $P^TAP$, and $P^TBP$ are all diagonal.

Since $$ A^{-1}B=A^{-1/2}CA^{1/2}, \quad C:=A^{-1/2}BA^{-1/2}, $$ where $C$ is SPD, we have $Q^TCQ=D$ for some orthogonal $Q$. Now set $P:=A^{-1/2}Q$ and verify that $$ P^{-1}A^{-1}BP=Q^TA^{1/2}A^{-1}BA^{-1/2}Q=Q^TCQ=D. $$ We have $P^TAP=Q^TA^{-1/2}AA^{-1/2}Q=Q^TQ=I$ and $P^TBP=Q^TA^{-1/2}BA^{-1/2}Q=Q^TQ=D$.

Note that $B$ does not need to be positive definite.

Answer 2

If your statement was true it would lead to a contradiction. Take $A=B\succ 0$ to be an arbitrary positive definite matrix, then in this case $A^{-1}B=I$ and for any invertible $P$ we would get $P^{-1}A^{-1}BP=I$. Using the conjectured statement, we would then conclude that $P^{T}AP$ is diagonal which is a contradiction due the arbitrary choice of $A\succ0$ and $P$.

Answer 3

This is treated in detail in Horn and Johnson; it is their method for finding both $Q^T AQ$ and $Q^T B Q$ diagonal.

The way you stated it is almost true. $P^T AP$ and $P^T B P$ may not be diagonal. However, in those locations where either one fails to be diagonal, the other one has a scalar multiple of the same square block. As a result, if necessary, there is an extra adjustment matrix $W$ to finish the job for both, that is both $W^T P^T APW$ and $W^TP^T B PW$ really are diagonal.

It works without extra effort in this one: Simultaneous Diagonalization of two bilinear forms

One needing extra effort: Congruence and diagonalizations Note that, while user1551 did the extra step with orthogonal matrices, this was not necessary. For a fixed, symmetric, square matrix (or block) of integers, call it $M,$ there is a quick way to solve $V^T MV$ diagonal, with $V$ all rational entries with determinant $1.$ For this problem, the theorem is that the same $V$ works for both matrices... reference for linear algebra books that teach reverse Hermite method for symmetric matrices

For illustration,.here is the square block that needs extra work in the answer by user1551, with my method:

$$ \left( \begin{array}{rr} 1 & 0 \\ -2/5 & 1 \end{array} \right) \left( \begin{array}{rr} 5 & 2 \\ 2 & 4 \end{array} \right) \left( \begin{array}{rr} 1 & -2/5 \\ 0 & 1 \end{array} \right) = \left( \begin{array}{rr} 5 & 0 \\ 0 & 16/5 \end{array} \right) $$

This is pages 229 and 231-232 in the first edition, anyway Theorem 4.5.15. I really like their Table 4.5.15T on page 229.