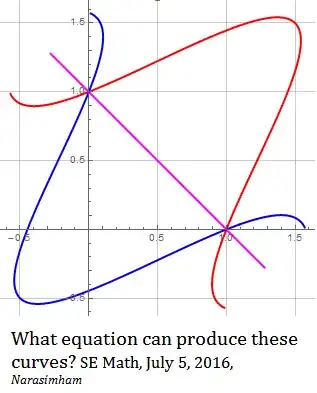
Does an equation exist that can produce the curves shown in the attached image, by varying a single variable?

Does an equation exist that can produce the curves shown in the attached image, by varying a single variable?

Consider the equilateral hyperbola $xy=1$ and map the points $(1,0)$ and $(0,1)$ to two symmetrical points on the hyperbola $(t,t^{-1})$ and $(t^{-1},t)$ by translation/scaling (as if you were zooming in).
$$(x(t-t^{-1})+t^{-1})(y(t-t^{-1})+t^{-1})=1.$$
The straight line corresponds to two infinitely close points, $t=t^{-1}=1$, which is a degenerate case of the equation.
Previous answer:
You can think of a pencil of parabolas, $y=\frac1{\sqrt2}+\frac\lambda{\sqrt2}(2x^2-1)$, which you rotate by $45°$ right, giving
$$x+y=1+\lambda\left((x-y)^2-1\right).$$
You can solve the quadratic equation for $y$.
Assuming what you drew to be a parabola, and $p$ a constant to push each parabola along the line of symmetry,
$$ y = p (1-x^2) $$
Now rotate them clockwise by $\pi/4 \, , (x,y) \rightarrow ( x+y, x-y)/\sqrt2. $
EDIT1:
As you left it free as regards shape within constraints, we could use a cosh curve, sec curve etc.
In fact, we can generalize this using any open even function E(x) , passing through $(\pm 1/\sqrt{2},1/\sqrt{2} ). $
Letting
$$y(x,p) = (1 + p *(1/2 - x^2) E(x)) /\sqrt{2} \, $$
and building a differentiable function, rotating the curve by $-\pi/4$, we can make the family pass through singular points $(0,1),(1,0) $as shown above and illustrated below in a particular case.
In graph below $E(x) = \cos^2(x) $is chosen with $ p= (\pm 2,0). $
For the earlier special case you got parabolas using $E(x)=1 $ perturbed by arbitrary $p$ values.
Try a superellipse: $|x|^a + |y|^a =1$ with $0 <a \le 1$.
Try also a quadratic Bézier curve $$ \gamma(t) = (1 - t)^{2} P_0 + 2(1 - t)t P_1 + t^{2} P_2 $$ where $P_0=(1,0), P_1=(a,a), P_2=(0,1)$, with $a \in [0,0.5]$.
You can first of all use a tool such as Engauge Digitizer to obtain tables of data points for each curve. Then either try a Log-log plot to determine a polynomial approximation or use a fitting tool of your choice to obtain fits of the same kind for each curve. Finally, find a parameter describing each curve such that all the fit-parameters previously obtained can also be fitted by simple functions, ideally linear or a low-order polynomial.
Use Lagrange Interpolation formula: For a variable point $(t,t)$ on the line $x-y=0$ with $0<t\leq \sqrt2/2$, fit a degree 2 polynomial curve that passes through the three points $(0,1), (t,t)$ and $ (1,0)$.
For $t=\sqrt2/2$ the three points will be collinear and it will automatically give a straight line. This must produce the same result as Yves Daoust's answer above, but using different interpretation.