I want to know if the way I derived the surface area of a sphere by integration is correct?

Question

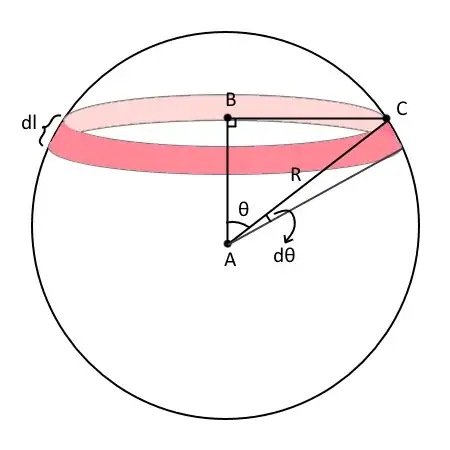
I am using the alias of Sillysack Buttowski and this is my first question. I searched on other links on stack exchange regarding "how to find the surface area of a sphere by integration". They seemed overly complex to me and not what I was searching for. Hence, I decided to post my own question.

Okay, so this is what I came up with: The calculation of the surface area of a sphere by integration and diagrams

Now, in the image I wrote that the limit of $dr$, as $dr$ approaches $0$ is equal to the circumference of the circle or $2\pi r$. I imagine that the sphere is made up of thin slices of circles where $dr$ is their thickness. Therefore, I integrated the integrand from $0$ to $2r$ and got the correct answer of $4\pi r^2$. Now is this correct? I doubt this is. It's too simple to be right. calculus is a difficult subject. Therefore, I can only infer that my answer may be correct, however, the way I got to answer is wrong, probably.

Now, I want any criticism you have and to tell me the holes and errors of my thought processes. By the way, I am not an expert in calculus as you can see. Thanks for your help in advance!

EDIT: Okay, so the $lim$ of $dr$ as $dr$ approaches $0$ is equal to $0$. The Circumference and $2\pi r$ are not related in anyway to it. So just cut off that part over there.

I don't get it. When $dr$ approaches $0$, then $dr$ approaches $0$, not $2\pi r$ — pajonk, Jun 18 '16 at 10:44
"I wrote that the limit of dr, as dr approaches 0 is equal to the circumference of the circle or 2πr" Huh?!!?!?!?! $\lim_{dr \rightarrow 0} dr = 0$. It has to equal 0. By tautological definition $\lim_{x \rightarrow \text{FishyPoopyFace} }x $ MUST = $ \text{FishyPoopyFace}$. $x \rightarrow Q$ MEANS $\lim x = Q$. — fleablood, Jun 19 '16 at 15:57
Why does the integrand go from 0 to 2pi r. The radii of the little strips go from 0 to R (R is the constant radius of the sphere, not the intermediate radii of the little circles). Not 0 to 2pi r. that's the half sphere. So you want $2\int_0^R 2\pi r dr$. Except that implies the radius and the height are equal. So this is the surface area of a double cone. Instead the relationship between height and radius is $r=\sqrt{R^2-h^2}$. So you want$2\int_0^R2\pi\sqrt{R^2-h^2}dh$. — fleablood, Jun 19 '16 at 16:10
I guess that the method above is wrong and not rigorous. However, the one given by Max Payne is really great and rigorous. Plus easy to understand, well, that is for me atleast. — Sillysack Buttowski, Jun 20 '16 at 11:29

Intelligenti pauca · Answer 1 · 2016-06-18T14:20:31.917

4

First of all you should use a clearer notation. For example: you cannot use $r$ to denote both the radius of the sphere and the integration variable. If I understand what you are trying to do, you want to calculate the surface area of a sphere by summing up the areas of the tiny strips comprised between two planes, perpendicular to a diameter of the sphere. There is nothing wrong with that and it is the very method Archimedes used a long time ago.

Let's call $x$ (and not $r$) the distance of the first plane from one end of the diameter, and $dx$ the distance between planes. The idea now is to compute the area of the strip to first order in $dx$. The result, however, is not $2\pi x\,dx$ (your result), but it is instead $2\pi r\, dx$.

To see why, look at the picture below: the area of the strip (to first order in $dx$) is $dA=2\pi\, l\cdot h$, where $h$ is different from $dx$. But by similarity of yellow and green triangles one has: $$ h:dx=r:l,\quad\hbox{that is:}\quad l\cdot h= r\cdot dx, $$ so that $dA=2\pi\,r\cdot dx$. Integrate now from $x=0$ to $x=2r$ and you are done.

edited Jun 18 '16 at 14:20

answered Jun 18 '16 at 11:07

Intelligenti pauca

50,470
4
42
77

Nope, can't figure it out. As I said I am not a calculus expert. It's much more of the opposite to that. Also, if you have the time, could you explain what you are saying in more detail? – Sillysack Buttowski Jun 18 '16 at 12:57
Just edited my answer. – Intelligenti pauca Jun 18 '16 at 14:06
I remember watching a video by Dr. James Tanton which used a similar method. Definitely a nice approach(+1) – Max Payne Jun 18 '16 at 14:57
for the very nice figure.

Paramanand Singh

Jun 19 '16 at 12:31

Okay, but why is $h:dx=r:l$? Why are the ratios equal? Why are they there in the first place? – Sillysack Buttowski Jun 22 '16 at 06:37

Do you want to know why the triangles are similar? Or something else? – Intelligenti pauca Jun 22 '16 at 15:35

Yes. I want to know why the triangles are similar. – Sillysack Buttowski Dec 18 '16 at 13:33

When $dx$ is very little, then hypotenuse $h$ is directed along the tangent (this is exact in the limit $dx\to0$), so $h$ is perpendicular to radius $r$. On the other hand, $dx$ is perpendicular to $l$: it follows that angles $\angle h,dx$ and $\angle r,l$ are equal and the triangles are similar. – Intelligenti pauca Dec 18 '16 at 15:00

score 2 · Accepted Answer · edited Apr 13 '17 at 12:21

2

Since you need the surface area, it would be more neat to take the area element spherically rather than linearly. It may also lead to errors : see Why can't I use the disk method to compute surface area?

Consider a sphere of radius $R$, and also consider an axis passing vertically through the centre of the sphere.

Now consider an Area element $\rm dS$ (pink ribbon) on the sphere inclined at $\theta$ angle from the axis, and subtending $\rm d\theta$ on the centre of sphere. Let the thickness of this area element be $\rm dl$.

When you open up this ribbon, we get a rectangle with width $\rm dl$, and length $= \rm2\pi\times BC$. The area of this rectangle is same as area of the elementary slice on sphere, ie, $\rm dS$

$$\rm dS=2\pi \text{BC}\times dl$$

Using the definition of angle in radians, we can calculate $\rm dl$ is: $$\rm \theta = \dfrac{\text{arc length}}{radius} \\ d\theta = \dfrac{dl}{dR} \\ \therefore\rm dl = Rd\theta$$
For calculating $\rm BC$, consider the right triangle $\rm ABC$. $$\rm \sin\theta = \dfrac{BC}{AC} = \dfrac{BC}{R}\\ \therefore BC = R\sin\theta$$

$$\rm\therefore dS=2\pi R\sin\theta\times Rd\theta$$

Then we integrate this element a complete angle of $\pi$ radians.

$$\rm S = \int_{0}^{\pi}2\pi R^2\sin\theta\times d\theta$$

$$\rm =2\pi R^2(1-\cos\pi)$$

$$\rm S=4\pi R^2$$

edited Apr 13 '17 at 12:21

Community

1

answered Jun 18 '16 at 11:10

Max Payne

3,447

And I just realised that I really need to learn some advanced trigonometry. I can't even understand what you wrote. Well, I guess this means I'll be postponing this question until I can understand what you just answered. – Sillysack Buttowski Jun 18 '16 at 12:59
Please don't say it like I'm really bad at trigonometry. Up until a few months ago I didn't even know that you could measure angles in radians. This radian system is still new for me, and the basic trigonometric functions and their reciprocals are all I know. I'll try to understand this slowly and eventually get it. – Sillysack Buttowski Jun 19 '16 at 13:01
Also, what does it mean that the length of area element is $2 \pi R sin {\theta}$, why is $\sin {\theta}$ there? – Sillysack Buttowski Jun 19 '16 at 13:18
I have added more details. I hope you get a better idea now! You can refer to articles on Wikipedia for trigonometric relations and identities: Trigonometry - Wikipedia – Max Payne Jun 19 '16 at 15:47
Wow, really thanks a lot. It is much clearer now and I understand all of it. I guess the previous one wasn't too well written such that I couldn't understand it. Well one last question, why is there no $dx$ term in the intergral? – Sillysack Buttowski Jun 20 '16 at 11:24
Because you are integrating over the surface! It not linear, do you see? What you did was integrate linearly, in one direction ($x$ in your case). But that method doesn't fit too well when calculating surface area. Its a very simplified solid angle integration: Read here Solid Angle - WIkipedia – Max Payne Jun 20 '16 at 11:41
Could you also tell me how you integrated $$\int_{0} ^{\pi} 2 \pi R^2 \sin {\theta}\ d\ {\theta}$$ I mean the steps of solving the integral. Explain as you would to a beginner. – Sillysack Buttowski Jun 20 '16 at 19:36
Take $2\pi R^2$ out of the integral, as it is constant. Now you know $$\int \sin \theta d\theta = -\cos\theta$$ Take minus sign out and now apply the limits of integration (upper limit minus lower limit). You get $$-(\cos \pi - \cos 0) = -(-1-1) = 2$$ And multiply it with the constant that you initially took common, ie, $2\pi R^2$. – Max Payne Jun 21 '16 at 05:28
Yes, I get it now. Is it possible to calculate the volume of a sphere and the surface area of a cone using this method or is another method preferred? I have been trying to calculate both of these by the above method with no luck. It just doesn't work, at least for me. Also, how do you know when you are working linearly or not? – Sillysack Buttowski Jun 22 '16 at 05:46
There are many ways for calculating volume. for cone, you can take linear slices and integrate along the axis of cone, or you can also use ring method. This site is a good place for learning that: www.math.lamar.edu/... – Max Payne Jun 22 '16 at 12:36
Yes, but how do you know when we are integrating linearly or not? – Sillysack Buttowski Jun 23 '16 at 06:01
It actually comes from approximation. We can integrate linearly in case of surface area too, provided we approximate properly. Look at aretino's answer. As he highlighted, there $dx$ was different from $h$, and approximating $h$ to $dx$ makes a difference. – Max Payne Jun 23 '16 at 08:40

I want to know if the way I derived the surface area of a sphere by integration is correct?

2 Answers2

Linked