2

I hope you can help me with the following, probably rather complex dilemma: I generally want to find an ellipse given two points and their respective tangents in 2-D space (X and Y coordinates). Now this question has already been answered on this forum here, with the answer that there exists an infinite number of ellipses satisfying these criteria.

I do have a set of data point pairs along with their respective tangents for each of which I want to find a unique ellipse for. Now this is impossible, as stated above, so I want to utilize boundary conditions to find the most probable, unique ellipse out of the infinite solutions for each data point pair (and their tangents). How I want to do this would probably lead too far, I just wanted to mention it in order to provide my motivation for the question below.

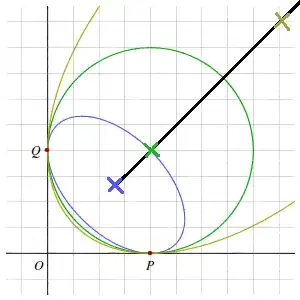
To this end I would like to identify the mechanisms underlying each set of infinite ellipses corresponding to each pair of data points and their tangents. I believe the key to this end is the development of the ellipse center points. Below you can find an altered version of the image kindly provided by the user Rahul in response to the question linked above, basically highlighting the infinite number of ellipses that pass through the points P and Q while sharing the same tangents.

enter image description here

As you can see in this case the center points of all ellipses lie on a line. I believe by finding the center point equation for each of my data point pairs I will be able to choose the appropriate center point for each pair, in turn allowing me to find a unique solution as I now have 5 pieces of information (two points, two tangents, one center point).

So much for background. Now: How do I go about achieving this? My ellipses will most likely be off-centered and angled. We can further assume that the slope of my tangents for each data point pair will never be equal, so there will always be a center point shift of some sort for the infinite solutions.

What I have found so far is the general solution for 2-D ellipses:

$$A x^2 + 2 B x y + C y^2 + 2 D x + 2 E y + F = 0 \qquad(1)$$

And an expression involving the slope/tangent m at each point (x,y) taken from an answer by user Blue to this question:

$$A x + B( y + x m ) + C y m + D + E m = 0 \qquad(2)$$

Unfortunately I could neither find nor derive an equation for the calculation of the center point of a tilted, off-centered ellipse. With my rather basic understanding of math reaching its limits at a question this complex, I would hence like to know:

  1. What is the general formula for the center of a tilted, off-centered ellipse?

As I further believe that solving this analytically will be a rather huge mess, through which I wouldn't want to ask anyone else to wade:

  1. What simplifications can I make in order to solve this analytically [e.g. (1) for P1 (x1,y1) - (1) for P2 (x2,y2) in order to remove F], without risking that my entire calculation unravels a few hours in to 0 = 0?

If this question is not well-enough explained please ask away, I will do my best to describe the issue as good as possible.

Community
  • 1
J.Galt
  • 197
  • What information do you have for one ellipse? – mvw Jun 13 '16 at 13:33
  • I have the following information: point 1 (x1,y1), point 2 (x2,y2), slope of tangent at point 1 (m1) and slope of tangent at point 2 (m2) – J.Galt Jun 13 '16 at 13:54
  • It's simple. Extend the tangents from $P$ and $Q$ to the point they intersect, call it $O$. Complete the parallelogram $QOPR$ to get the fourth point $R$ (in your diagram, it's the green cross). The centers lie along the line through $O$ and $R$. –  Jun 13 '16 at 14:05
  • Thanks for the response, I thought about that as well. I am however not sure whether the centers will always lie on a linear graph, or whether this is a special case resulting from the fact that the tangents intersect orthogonally. – J.Galt Jun 13 '16 at 14:25
  • 1
    Under any non-degenerate affine transform: $(x,y) \mapsto (ax+by+c,dx+ey+f)$ with $ae-bf \ne 0$, ellipses get mapped to ellipses and so do their centers. You can use an affine transform to first bring $\angle POQ$ to $90^\circ$ and then another affine transform to bring $|PO| = |OQ|$. It is clear after the transform the centers of the ellipses tangent to $OP$ at $P$, $OQ$ at $Q$ form a straight line. Now apply inverse transform, you find the centers of your original family of ellipses lie on a straight line. – achille hui Jun 13 '16 at 15:13
  • Thank you very much for your response. If they always form a straight line then my problem is almost solved. Now I need help with one last thing: How can I find the unique ellipse from two points, the tangents at these points, and their center point? Shall I open a new question for this? – J.Galt Jun 13 '16 at 15:23
  • Ellipses are symmetric with respect to their center. If $p$ is a point on an ellipse centered at $c$, then $2c - p = c - (p-c)$ is also lying on same ellipses. Start from the original two points and their tangents, if the two points are not collinear with the center, their image will be two extra points on the ellipse. Since having tangent at a point is equivalent to have two nearby points on the ellipse, you now have 6 points (2 old + 2 from tangent + 2 new) for your ellipse. – achille hui Jun 13 '16 at 16:32

1 Answers1

1

As achille hui wrote in a comment, your setup is invariant under affine transformations. So you can simplify things by choosing an affine coordinate system in such a way that the tangent lines meet at $(0,0)$ and the points of contact are $(1,0)$ and $(0,1)$. In that case, for reasons of symmetry the centers of all your ellipses have to lie on the line $x=y$. If you have such a center located at $(c,c)$, the ellipse you are after has the equation

$$(x, y, 1)\cdot\begin{pmatrix} -c & c-1 & c \\ c-1 & -c & c \\ c & c & -c \end{pmatrix}\cdot\begin{pmatrix}x\\y\\1\end{pmatrix}=0$$

according to my computations (but please verify). To transform this conic back to your original coordinate system, you have to conjugate this matrix with the transformation matrix (in homogeneous coordinates, i.e. a $3\times3$ matrix) which transforms from original to simplified coordinate system.

MvG
  • 42,596