I'm attempting to generate an ellipse for a stair simulation game of mine, and the inputs are:
I've heard that these five items are enough to generate an ellipse equation - how is it done? Also, how can it be put into $f(x)$ format?
Thanks in advance for any help!
The equation of a general conic section has the form $$A x^2 + 2 B x y + C y^2 + 2 D x + 2 E y + F = 0 \qquad(\star)$$ where the condition $B^2 - AC < 0$ indicates an ellipse. Implicit differentiation gives a relation involving the slope (which I'll write as $m$) at the point $(x,y)$: $$A x + B( y + x m ) + C y m + D + E m = 0 \qquad(\star\star)$$
Your inputs include three points (say, $P_0 = (x_0, y_0)$, $P_1 = (x_1, y_1)$, and $P_2 = (x_2,y_2)$) and two slopes-at-points (say, $m_1$ at $P_1$, and $m_2$ at $P_2$). These give you three particular instances of $(\star)$, and two of $(\star\star)$; that's five linear equations in the six unknowns $A$, $B$, $C$, $D$, $E$, $F$. Having a spare unknown isn't so bad here, since the system of equations is homogeneous; effectively, we can divide-through by one of the unknowns, reducing the count to five.
Solving the system is easy enough to do numerically (which you could probably do within your simulation program), and usually fairly ugly to do symbolically. As has been mentioned in a comment, since an ellipse is not the graph of a function, it can't be "put into $f(x)$ format" ... at least, perhaps not in the way you might be thinking. However, if you use polar coordinates, and make the assumption that, say, $P_0$ lies at the origin, then you can arrive at not-too-horrible symbolic equation for the ellipse.
In what follows, I take $P_0$ to be the origin. (Note that this gives us $F=0$ immediately.) We'll give our other points polar coordinates, $P_i = (r_i, \theta_i)$, and we'll also express the slopes at these points in terms of angles: $m_i = \tan\phi_i$.
With $F=0$, we find that the polar form of $(\star)$ ---derived with the substitutions $x = r\;\cos\theta$ and $y = r\;\sin\theta$--- has a factor of $r$ representing the solution-point of the origin itself. Solving the other factor for $r$ gives this polar equation for the conic section
$$r = \frac{- 2\left( D\cos\theta + E\sin\theta \right)}{A\cos^2\theta + 2 B\cos\theta\sin\theta+C\sin^2\theta}$$
We have therefore put the conic in "$r = f(\theta)$ format".
Now, having tediously solved for coefficients $A$ through $E$, it turns out that the above becomes
$$r = \frac{r_1 r_2 \sin\Delta \left( \begin{array}{c} \phantom{-} r_1 \sin\Delta_1\; (\;\cos(\theta-\phi_2) \cos\Delta - \cos((\theta-\theta_1)-\Delta_2) \;) \\ - r_2 \sin\Delta_2\; (\;\cos(\theta-\phi_1) \cos\Delta - \cos((\theta-\theta_2)-\Delta_1)\;) \end{array} \;\;\right)}{\sin\Delta_1 \sin\Delta_2\; (\;r_1 \sin(\theta-\theta_1) - r_2 \sin(\theta-\theta_2)\;)^2 - r_1 r_2 \sin(\theta-\phi_1)\sin(\theta-\phi_2) \sin^2\Delta}$$ where $\Delta = \theta_1-\theta_2$ and $\Delta_i = \theta_i - \phi_i$.
The condition $B^2-AC < 0$ for the curve to be an ellipse reduces to:
$$\begin{align} &\;4 \; \sin(\theta_1-\phi_1) \;\sin(\theta_2-\phi_2) \\ &\;\;\cdot\left(\; r_1 \sin(\theta_1 - \phi_1) - r_2 \sin(\theta_2 - \phi_1) \;\right) \\ &\;\;\cdot\left(\; r_1 \sin(\theta_1 - \phi_2) - r_2 \sin(\theta_2 - \phi_2) \;\right) \\ &+ r_1 r_2\;\sin^2(\theta_1-\theta_2)\;\sin^2(\phi_1 - \phi_2) \qquad<\; 0 \end{align}$$ where $r_1$, $r_2$ are assumed strictly positive, and angles $\theta_1$ and $\theta_2$ are distinct. (Otherwise, append the factor $r_1 r_2 \sin^2(\theta_1-\theta_2)$ to the left-hand side.)
(Aside: The above was derived through fairly arduous and mechanical symbol manipulation, but the final result seems as though it wants to say something profound about the geometry of the situation. Hmmmm ...)
So, for example, given polar inputs ... $$P_0 = (0,0)\qquad P_1 = \left(1,\frac{\pi}{3}\right) \qquad P_2 = \left(2,-\frac{\pi}{4}\right) \qquad \phi_1 = \frac{\pi}{6} \qquad \phi_2 = -\frac{\pi}{6}$$
... the result is this ellipse:
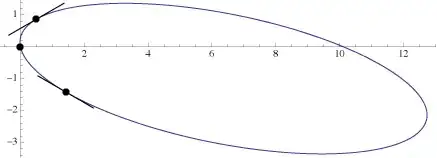
You can't put an ellipse in a f(x) format because it's not a function. (An ellipse is round; for nearly every x value in the ellipse, there are two corresponding y values.) You could put half of an ellipse in a f(x) format, however.\\
I would approach this problem by first writing out the equation for an ellipse in its most general form. Figure out what parameters you need to find out in order to fully define the ellipse. Then, see if you can come up with equations using the pieces of information you're given, in terms of these parameters.