Prove $(x+y)(y^2+z^2)(z^3+x^3) < \frac92$ for $x+y+z=2$

Question

$x,y,z \geqslant 0$ and $x+y+z=2$, Prove $$(x+y)(y^2+z^2)(z^3+x^3) < \frac92$$

While numerical method can solve this problem, I am more interested in classical solutions. I tried this problem for the past few months, using all kinds of AM-GM and CS, but still cannot solve it. I hope someone can help me out with this one.

Answer 1

Here is a rather ugly proof (but with the side benefit to get the maximum analytically):

• $z=0$, $x+y=2$; apply AM-GM: $$(x+y)y^2x^3=2x^3y^2=6^3\left(\frac{x}{3}\right)^3\left(\frac{y}{2}\right)^2\le6^3\left(\frac{x+y}{5}\right)^5=\left(\frac{24}{25}\right)^2\left(\frac{12}{5}\right)<\frac{9}{2}.$$

• $z>0$, let $x=az,~y=bz$, constraint becomes $(a+b+1)z=2$. eliminate $z$: $$(x+y)(y^2+z^2)(z^3+x^3)=z^6(a+b)(b^2+1)(a^3+1)=\frac{64(a+b)(a^3+1)(b^2+1)}{(a+b+1)^6}=:f(a,b).$$ To get $$\max_{a,b\ge0}~f(a,b),$$ consider the following two cases:

  1. $s=a+b\ge1$, where the inequality is weak; apply AM-GM and $a,b\le s,$ $$(a^3+1)(b^2+1)=3^32^2\left(\frac{a}{3}\right)^3\left(\frac{b}{2}\right)^2+a^3+b^2+1<3^32^2\left(\frac{s}{5}\right)^5+s^3+s^2+1,$$ thus $$f<\frac{5s^6+128(s^4+s^3+s)}{2(s+1)^6}<\frac{7}{2}<\frac{9}{2},$$ as $$\frac{3^32^2}{5^5}<\frac{5}{128}$$ and $$7(s+1)^6-[5s^6+128(s^4+s^3+s)]\\=2s^6+19s^5+12s^3+19s^2+7+s(s-1)(23s^3+86)>0.$$
  2. $s=a+b<1$, thus $a,b<1$ and given $s$, $$(a^3+1)(b^2+1)=1+b^2+a^3+a^3b^2\le1+b^2+a^2+2ab=1+s^2,$$ or $$f\le\frac{64s(1+s^2)}{(1+s)^6}<4.4772<\frac{9}{2},$$ where the maximum is achieved at $a=0$ and $b=s\approx0.223$, the only real root of the cubic equation $3t^3-3t^2+5t-1=0$. They are equivalent to $z\approx1.635$ (the real root of $3t^3-10t^2+12t-6=0$), $x=0$ and $y=2-z\approx0.365$.

---

Post-mortem:

• Is there an elementary way to prove that the maximum of $64s(1+s^2)(1+s)^{-6}$ is less than $9/2$? I had to take the derivative and solve the resulting cubic equation numerically;
• By rescaling, the homogeneous version is $$(x+y)(y^2+z^2)(z^3+x^3)<\frac{9}{2}\left(\frac{x+y+z}{2}\right)^6,$$ for $x,y,z\ge0$ and the coefficient on RHS can be improved to ~$4.4772$ as above.

Answer 2

Let $f(x,y,z)=(x+y)(y^2+z^2)(z^3+x^3)$.

Assume that $y$ is largest of $x,y,z$. Then $$f(x,y,z)-f(x,z,y)=(y^2+z^2)(x + y) (x + z) (y - z) (x - y - z)\le0$$and therefore we may assume $x$ or $z$ is largest of $x, y, z$.

If $x$ is largest, then $$f(x,y,z)-f(z,y,x)=(z^3+x^3)(z-x)(xy+xz-y^2+yz)\le0$$and therefore we may assume that $z$ is largest of $x,y,z$.

Now,$$f(0,x+y,z)-f(x,y,z)=(x+y)(((x+y)^2+z^2)z^3-(y^2+z^2)(z^3+x^3))\\=x (x+y)(-x^2 y^2 - x^2 z^2 + x z^3 + 2 y z^3)\ge0$$and we may assume that $x=0$. Now it is just $y(y^2+(2-y)^2)(2-y)^3<\frac{9}{2}$, or$$2 y^6 - 16 y^5 + 52 y^4 - 88 y^3 + 80 y^2 - 32 y + 4.5>0$$which is true for all nonnegative $y$.

Answer 3

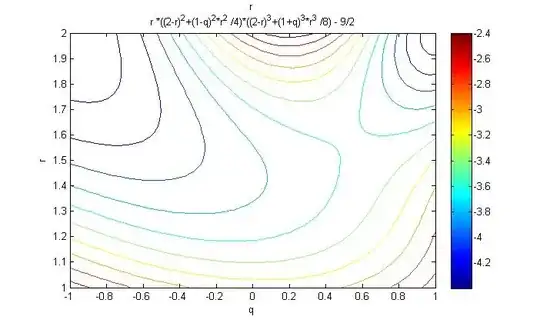
Problem conditions allows us to eliminate the variable $x$ and to seek the unconditional maximal value of function $$f(y,z)=(2-z)(y^2+z^2)(z^3+(2-y-z)^3).$$ Let $t=2-z,$ then $$x=t-y,\quad z=2-t,$$ $$f(y,t)=(y^2t+t^3-4t^2+4t)((t-y)^3 + (2-t)^3),$$ $$0<y<t<2.\qquad (*)$$ Nesessary conditions of maximum within the area are $$\begin{cases} f'_y = 2yt\left((2-t)^3+(t-y)^3\right) + (y^2t+t^3-4t^2+4t)(-3)(t-y)^2 = 0\\ f'_t = (y^2+3t^2-8t+4)\left((2-t)^3+(t-y)^3\right) + (y^2t+t^3-4t^2+4t)(-3)\left((t-2)^2-(t-y)^2)\right) = 0 \end{cases}$$ $$\begin{cases} 2y\left((t-y)^3-(t-2)^3\right) -3(t-y)^2\left(y^2+(t-2)^2\right) = 0\\ (y^2+3t^2-8t+4)\left((t-y)^3-(t-2)^3\right)- 3t\left(y^2+2ty-4t+4)\right)\left(y^2+(t-2)^2\right) = 0 \end{cases}$$ This system is a homogeneous linear system for the variables $\left((t-y)^3-(t-2)^3\right)$ and $\left(y^2+(t-2)^2\right)$. 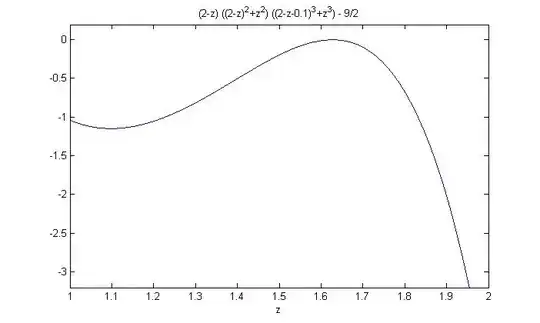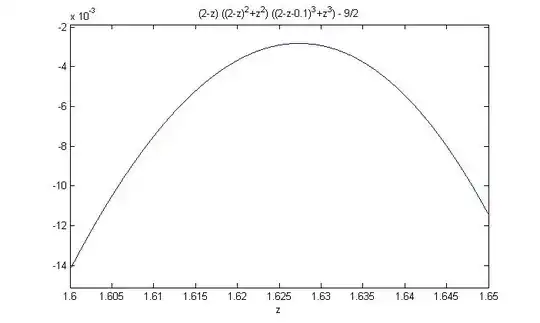The condition of existence of nonzero solutions of the form $$\Delta=0,$$ $$\Delta=\begin{vmatrix} 2y & (t-y)^2\\ y^2+3t^2-8t+4 & t(-y^2+2ty-4t+4) \end{vmatrix}$$ So $$\begin{cases} 2yt(-y^2+2ty-4t+4) - (t-y)^2(y^2+3t^2-8t+4) = 0\\ 2y\left((t-y)^3-(t-2)^3\right) -3(t-y)^2\left(y^2+(t-2)^2\right) = 0\\ \end{cases}.$$ As shown in attachment, the maximum value of the objective function among the extreme points reached when $$(x,y,z,f)=(0.272109,0.066672,1.661219,4.311784),$$ or $$(t,y,f)=(0.338781, 0.0666722, 4.31178).$$ It is easy to see that this point is a solution both the first and the second equations.

Verify the edges of area.

If $y=0$ then $$f(t)=(t^3-4t^2+4t)(t^3+(2-t)^3) = 6t^5-36t^4+80t^3-80t^2+32t,$$ $$f'(t)=30t^4-144t^3+240t^2-160t+32 = 2(t-2)(15t^3-42t^2+36t-8).$$ Real root of $(15t^3-42t^2+36t-8)$ equals to $$t_m=-\dfrac2{15}(-7+2^{1/3}+2 2^{2/3})\approx 0.34204,$$ $$f(t_m)=\dfrac{64 \left(376+92\cdot2^{1/3}+89\cdot2^{2/3}\right)}{9375}\approx4.32259.$$

(Updated)

If $t=y$ then $$f(t) = (2t^3-4t^2+4t)(2-t)^3 = -2t^6 + 16t^5 - 52t^4 + 88t^3 - 80t^2 + 32t,$$ $$f'(t) = -12t^5 + 80t^4 - 208t^3 + 264t^2 - 160t + 32 = -4(t-2)^2(3t^3-8t^2+8t-2),$$ $$f(t)=\dfrac1{81}\left(-54t^3+288t^2-492t+260)(3t^3-8t^2+8t-2)+112t^2-472t+520\right)$$ Real root of $(3t^3-8t^2+8t-2)$ equals to $$t_{m1}=\dfrac19\left(8-\dfrac8{\sqrt[3]{27\sqrt{17}-109}}+\sqrt[3]{27\sqrt{17}-109}\right)\approx0.364976,$$ $$f(t_{m1})=\dfrac1{81}\left(112{t_{m1}}^2-472t_{m1}+520\right)\approx4.47717$$

If $t=2$ that $$f(y) = 2y^2(2-y)^3=-2y^5+12y^4-24y^3+16y^2,$$ $$f'(y) = -10y^4 + 48y^3 - 72y^2 + 32y = -2y(y-2)^2(5y-4),$$ $$(t,f) = \left(\dfrac45,\dfrac{6912}{3125}\right)\approx(0.8, 2.21184)$$

Account, that the values of function at the vertices of the area are zero.

Thus $$f(y,t)<4.4772$$ and therefore $$\boxed{(x+y)(y^2+z^2)(z^3+x^3)<\dfrac92\text{ for } x+y+z=2}$$

Completed 09.07.16

Attachment

The exact value of the maximum within the area defined by the system of two algebraic equations of the fourth order in two variables. We show how to present its solution through the roots of a polynomial in one variable. At first: $$\begin{cases} 2ty(2-y)(2-2t+y) - (t-y)^2(y^2+(3t-2)(t-2)) = 0\\ y(2-y)(2(2-t)^2+(2y-2t)(2-2t+y)) - (t-y)^2(3y^2+(3t-6)(t-2)) = 0, \end{cases}$$ $$\begin{cases} 2y(2-y)(-2t^2+(y+2)t) - (t-y)^2(3t^2-8t+4+y^2) = 0\\ y(2-y)((2-t)^2+(y-2t)(2-2t+y)) - (t-y)^2(y^2+2(2-t)) = 0.\quad [((2)-(1))/2] \end{cases}$$ $$\begin{cases} 3(t-y)^4 + 2(3y-4)(t-y)^3 + 4(t-y)^2 - 2y(y-2)(3y-2)(t-y) - 2y^2(y-2)^2 = 0\\ (t-y)^3 - (3y^2-6y+2)(t-y)^2 + y(2-y)(3y-4)(t-y) + y(1-y)(2-y)^2 = 0, \end{cases},$$ or $$\begin{cases} 3x^4 + (6y-8)x^3 + 4x^2 - 2y(y-2)(3y-2)x - 2y^2(y-2)^2 = 0\\ x^3 - (3y^2-6y+2)x^2 + y(2-y)(3y-4)x + y(1-y)(2-y)^2 = 0, \end{cases}.$$ Note that the first equation can be replaced for the remainder when divided by the second equation.
Given the identity of $$(ax^2+bx)c^2 = (acx+bc-ad)(cx+d)+(ad-bc)d\qquad(1)$$ for $$a=3,\quad b=6y-8,\quad c=1,\quad d=-(3y^2-6y+2),$$ the quotient of polynomials still $$q=3x+6y-8+3(3y^2-6y+2)=3x+9y^2-12y-2.$$ Therefore, $$3x^4+(6y-8)x^3+4x^2-2y(y-2)(3y-2)x-2y^2(y-2)^2-(3x+9y^2-12y-2)(x^3-(3y^2-6y+2)x^2+y(2-y)(3y-4)x+y(1-y)(2-y)^2\\ = 3y(9y^3-27y^2+18y+4)x^2 + 3y(y-2)(9y^3-23y^2+9y+6)x + y(y-2)^2(9y^3-21y^2+8y+2).$$

Within the area $y\not=0,$ so we have $$\begin{cases} P_2(y)x^2 + 3(y-2)P_1(y)x + 3(y-2)^2P_0(y) = 0\\ x^3 - (3y^2-6y+2)x^2 + y(y-2)(4-3y)x+ y(1-y)(y-2)^2 = 0, \end{cases}$$ where $$P_0(y) = 9y^3-21y^2+8y+2,$$ $$P_1(y) = 3(9y^3-23y^2+9y+6),$$ $$P_2(y) = 3(9y^3-27y^2+18y+4).$$ Within the area $y\not=2.$ Let $$x=(2-y)u,$$ then $$\begin{cases} P_2(y)u^2-P_1(y)u+P_0(y)=0,\\ (y-2)u^3 + (3y^2-6y+2)u^2 + (4y-3y^2)u + y^2-y = 0. \end{cases}$$

Quotient by dividing of the second polynomial with multiplier $P_2^2$ to the second polynomial can be calculated by the formula $(1)$ for the values $$a_1 = y-2,\quad b_1= 3y^2-6y+2,\quad c_1 = P_2(y),\quad d_1 = -P_1(y),$$ so it equals to $$q_1(u,y) = (a_1u +b_1)c_1-a_1d_1 = ((y-2)u + 3y^2-6y+2)P_2(y)+(y-2)P_1(y),$$ $$q_1(u,y) = 3(u(y-2)(9y^3-27y^2+18y+4) + 27 y^5-126y^4+193y^3-95 y^2-4))$$

Wherein $$P_2^2(y)\left((y-2)u^3 + (3y^2-6y+2)u^2 + (4y-3y^2)u + y^2-y)\right) - q_1(u,y)(P_2(y)u^2 - P_1(y)u + P_0(y))\\ = -3(81y^6-273y^5+132y^4+285y^3-94y^2-212y+56)u\\ + 3(18y^6+3y^5-263y^4+518y^3-278y^2-16y+8).\\$$

So $$\begin{cases} P_2(y)u^2-P_1(y)u+P_0(y)=0,\\ Q_1(y)u-Q_0(y) = 0,\\ \end{cases}$$ where $$Q_0(y) = 18y^6+3y^5-263y^4+518y^3-278y^2-16y+8,$$ $$Q_1(y) = 81y^6-273y^5+132y^4+285y^3-94y^2-212y+56.$$

At last, immediate using of $(1)$ gives $$Q_1^2(P_2u^2-P_1u) = q_1(y,u)(Q_1u-Q_0)+(-P_2Q_0+P_1Q_1)(-Q_0),$$ so we have a system $$\begin{cases} P_2(y)Q_0^2(y)-P_1(y)Q_0(y)Q_1(y)+P_0(y)Q_1^2(y)=0,\\ Q_1(y)u-Q_0(y) = 0,\\ \end{cases}$$ where the first equation $$28431y^{15}-332424y^{14}+1769283y^{13}-5834430y^{12}+13865013y^{11} -25972002y^{10}+39273849y^9-46208412y^8+39498804y^7-22289616y^6+6739136y^5-82304y^4-544960y^3+77312y^2+12544y-1024=0$$ depends only on the $y$ and for $y\in(0,2)$ has roots $$y_4=0.06667216, y_5=0.36405184, y_8=1.26087211, y_9=1.53077106, y_{12}=1.65191401,$$ full Mathcad results are:

That gives us the next solutions within the area $x,y,z>0:$ $$(x,y,z,f)\in\left\{ \begin{matrix} (0.272109,0.066672,1.661219,4.311784)\\ (1.217651,0.364052,0.418297,0.913705)\\ (0.229352,1.530771,0.239877,0.109307)\\ (0.164858,1.651914,0.183228,0.053358) \end{matrix} \right\}$$ Done!

It can be seen that using the algorithm for polynomials, similar the Euclidean algorithm, eliminates the second variable $x$ (or $u$), expressing it through the ratio of polynomials. Also it gives a polynomial equation for $y$.

Answer 4

The proof comes by considering three cases.

Case 1: $z>1$, $y> 0.1$. We have $$(x+y)(y^2+z^2)(z^3+x^3) - \frac92= (2-z)((2-x-z)^2+z^2)(z^3+(2-z-y)^3) - \frac92\\ < (2-z)((2-z)^2+z^2)(z^3+(2-z-0.1)^3) - \frac92$$ which is less than 0, see this plot: and in more detail here:

Case 2: $z>1$, $y\leq 0.1$. We have $$(x+y)(y^2+z^2)(z^3+x^3) - \frac92= (2-z)(y^2+z^2)(z^3+(2-z-y)^3) - \frac92\\ < (2-z)((0.1)^2+z^2)(z^3+(2-z)^3) - \frac92$$ which is less than 0, see this plot:

Case 3: $z \leq 1$. Here, let $x = \frac{r}{2} (1+q)$ and $y = \frac{r}{2} (1-q)$. Hence, $x+y = r$ and $1 \leq r \leq 2$. Further, $-1\leq q \leq 1$ since $x \geq 0$ and $y \geq 0$. With this notation, we have

$$(x+y)(y^2+z^2)(z^3+x^3) - \frac92= r (\frac{r^2}{4} (1-q)^2+(2-r)^2)((2-r)^3+\frac{r^3}{8} (1+q)^3) - \frac92$$ which is less than 0 in the given ($q,r$)-range, see this contourplot:

Note 1: since no upper limits have been made in rewriting the equation for case 3, it would have been possible to drop the condition $z\leq 1$ and, giving the proof without case discussion, to draw the contourplot for the full range $0\leq r \leq 2$. However, the delicate case where the bound is very tight occurs in case 1 and is easier to see with the given description in case 1. In a contourplot for the full range $0\leq r \leq 2$, this delicate case can only be shown with magnification of the relevant area.

Note 2: The first two cases are in one parameter $z$ only, so showing the negativity over the given $z$-range will be easily possible, instead of plots, by analytic approximations.

Note 3: In the third case, the values are manifestly negative in the whole considered range. Hence, also here, showing negativity over the whole range will be easily possible, instead of plots, by coarse approximations.

This completes the proof.