3

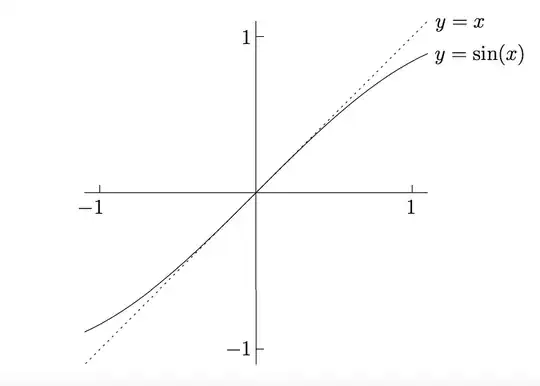
So I've learned that $\lim_{x \rightarrow 0}{\frac{\sin(x)}{x}} = 1$ is true and the following picture really helped me get an intuitive feel for why that is

enter image description here

I have been told that this limit is true whenever the argument of sine matches the denominator and they both tend to zero. That is,

$$\lim_{x \rightarrow 0}{\frac{\sin(5x)}{5x}} = 1$$

$$\lim_{x \rightarrow 0}{\frac{\sin(x^2)}{x^2}} = 1$$

$$\lim_{x \rightarrow 0}{\frac{\sin(\text{sin(x)})}{\text{sin(x)}}} = 1$$

But I don't understand why.

Question: Is there an intuitive explanation for why the rule $\lim_{x \rightarrow 0}{\frac{\sin(\text{small})}{\text{same small}}} = 1$ holds?

The picture above really helped me understand the original limit, but it doesn't really help me understand why the others are true.

ApprenticeOfMathematics
  • 472
  • I saw that as soon as I posted. I've made the change – ApprenticeOfMathematics May 22 '16 at 11:40
  • I believe that $x$ should be approaching $0$, not infinity. – Michael Burr May 22 '16 at 11:40
  • If you substitute $y=kx$, you immediately see, that $\frac{sin(kx)}{kx}$ tends to $1$ because if $x$ tends to $0$, $y$ tends to $0$ as well. This is also true for every continous function $y=g(x)$, where $g(0)=0$ – Peter May 22 '16 at 11:40
  • Well, it really works out that limit is equal to $1$ firstly. If it didn't, we'd be having some issues already. And the others are true as long as the arguments approach $0$ at the same rate. – Simply Beautiful Art May 22 '16 at 11:41
  • Would it help you if you simply made a substitution $y = \text{small}$? As long as small tends to zero as $x\to 0$ you get the limit $$\lim\limits_{y\to 0}\frac{\sin y}{y}, $$ which you already know is 1. It doesn't matter if the symbol is $y$ or $x$. The small thing just needs to tend to 0. – Eff May 22 '16 at 11:48
  • @Eff This comment helped the most. – ApprenticeOfMathematics May 22 '16 at 11:57
  • By small means infinitesimal and you know if $x\to 0\implies nx\to 0,,,n\in \mathbb N$ so if you replace $nx$ by $y$ then $y\to 0$ – user5954246 May 22 '16 at 11:59
  • @ApprenticeOfMathematics I'm glad it helped. – Eff May 22 '16 at 12:01
  • @ApprenticeOfMathematics My comment was quite similar. – Peter May 22 '16 at 12:13
  • 1
    @Peter It was, you detailed a similar idea, but I was unsure of how to use that to understand the limit with sin(x) as the argument (i.e. the third limit above under the graph). I was just thinking "how would I write sin(x) as kx?", but I agree that the idea is similar, thanks! – ApprenticeOfMathematics May 22 '16 at 12:17
  • @ApprenticeOfMathematics I added the idea with an arbitary continous $g(x)$ later, perhaps you overlooked that. – Peter May 22 '16 at 12:18
  • 1
    @Peter I did overlook this, which is my fault! Thanks for the comment man, I can see that this is equivalent to what Eff said. – ApprenticeOfMathematics May 22 '16 at 12:26

3 Answers3

4

This is because

  • $\lim_{x\to a}f(x)=b$

is equivalent to

  • $\lim_{n\to\infty}f(x_n)=b$ for every sequence $(x_n)_{n\in\Bbb N}$ with $x_n\to a$.
Hagen von Eitzen
  • 374,180
  • 1
    It might be useful for OP to know that the first one is called "Cauchy's definition" and the second one -- "Heine's definition". – Mihail May 22 '16 at 11:49
4

I'm not sure that this falls into the category of "intuitive explanation" but the general phenomenon you are considering is a consequence of the commutativity of composition of continuous functions and limits. If you let $f(x) = \frac{\sin x}x$, then for any continuous function $g$ with $g(0)=0$ we have $\lim_{x \rightarrow 0} f \circ g(x) =1$.

Martin Sleziak
  • 53,687
Josh R
  • 556
  • This is similar to the Eff comment above and is the best answer I received, so I will accept it. Thanks! – ApprenticeOfMathematics May 22 '16 at 12:00
  • :) you are most welcome – Josh R May 22 '16 at 13:29
  • We don't need continuity of $g$. What is needed is the fact that $g(x)$ tends to $0$ and that $g(x) \neq 0$. According to your answer if $g(x)$ is the constant $0$ function then also your result holds, but then $f\circ g(x)$ is not defined for any $x$. I wonder why the idea of continuity of $g$ is so prevalent. I have seen such unnecessary mention of continuity in many answers to similar questions. – Paramanand Singh May 23 '16 at 06:50
2

So we know (by know here I mean we know the proof) that the following is true $$\lim_{x \to 0}\frac{\sin x}{x} = 1\tag{1}$$ Now the symbol $x$ used here is a variable and it does not matter what value or quantity it represents as long as it tends to $0$. We can by a certain abuse of notation write the same equation in a crude manner as $$\lim_{\text{"small thing" tends to zero}}\frac{\sin(\text{"small thing"})}{\text{"small thing"}} = 1$$ In more formal terms let $f$ be a function of $x$ such that $$\lim_{x \to a}f(x) = 0\tag{2}$$ and $$f(x) \neq 0\tag{3}$$ as $x \to 0$. Then we can write the equation $(1)$ as $$\lim_{x \to a}\frac{\sin f(x)}{f(x)} = 1\tag{4}$$ whenever equations $(2), (3)$ hold.

That equations $(1), (2), (3)$ lead to equation $(4)$ is proved via the use of rule of substitution. The important idea to note is that $(\sin x)/x$ tends to $1$ as $x \to 0$ and it does not depend on the manner in which $x \to 0$. Thus for example $x^{2}$ also tends to $0$ as $x \to 0$ but it tends much faster and hence $(\sin (x^{2}))/x^{2}$ tends to $1$. Equation $(4)$ says the same thing that it does not matter how slow / fast / or in whatever manner the argument $f(x)$ of $\sin $ tends to $0$ the expression $(\sin f(x))/f(x)$ tends to $1$ as long as we ensure that $f(x)$ never actually becomes $0$ (because then the expression would be meaningless due to division by $0$). So the intuitive explanation of $(4)$ is ultimately dependent on intuitive explanation of $(1)$ (which you already mention in your question).

I am not sure why there is a prevalent idea that for equation $(4)$ to hold we must have $f$ continuous at $x = a$ (this is also mentioned in the accepted answer). This is not necessary at all. The "small thing" mentioned in the beginning is only supposed to tend to $0$ and not that it should tend to $0$ in a continuous manner.

Paramanand Singh
  • 87,309