What is the moment of inertia of a Gosper island?

Question

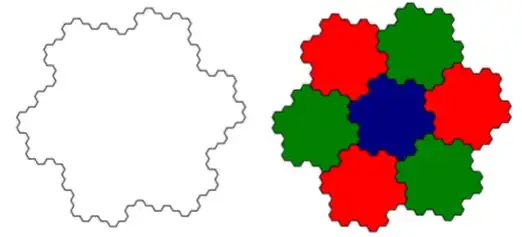
We know that regular hexagons can tile the plane but not in a self-similar fashion. However we can construct a fractal known as a Gosper island, that has the same area as the hexagon but has the property that when surrounded by 6 identical copies produces a similar shape, but with dimensions scaled by a factor of $\sqrt{7}$.

What is the distance between two of the centers? Is it the same as the distance between hexagons of the same area? ie. If I start with a hexagon of area A, then construct a Gosper island and place it next to an identical copy, would the distance still be the same as if they were hexagons? Or does the scaling factor come into play somewhere? Right now I think the answer is $\sqrt{3}/2$, as for the hexagon.

The reason I ask is that I'm trying to calculate the Gosper island's moment of inertia through an axis through its centre of mass and perpendicular to the plane of the island.

If we assume that the moment of inertia is always proportional to the mass, and proportional to the square of a characteristic length scale, then $$ I = \gamma Ml^2, $$ where $\gamma$ is a constant, $l$ is the 'diameter' of the island, in a hexagon this would be the distance between two opposite vertices. Shrink the Gosper island by the scaling factor and surround it by six others. This self-similarity technique is super cute, and can be used to calculate the moment of inertia of an equilateral triangle, and can be extended to a square/rectangle quite easily. Fractals, having a high degree of self-similarity, seem amenable to this technique - here I calculate the moment of inertia for a Koch snowflake.

$\hspace{1.3cm}$

Using the principle of superposition, $$ I = I_{\text{centre}} + 6I_{\text{edge}}, $$ where $$ I_{\text{centre}} =\gamma \frac{M}{7}\left(\frac{l}{\sqrt{7}}\right)^2 = \gamma \frac{Ml^2}{49} = \frac{I}{49}. $$

Now, by the parallel axis theorem $\displaystyle I_{\text{edge}} = I_{\text{COM}} + Md^2$ where $$ \displaystyle I_{\text{COM}} = \frac{I}{49} $$ and $\displaystyle d= \frac{\sqrt{3} l}{2} $ (this was one source of error), so $\displaystyle I_{\text{edge}} = \frac{I}{49} + \frac{3Ml^2}{4},$ and \begin{align*} I &= \frac{I}{49} + 6\left(\frac{I}{49}+ \frac{3Ml^2}{4}\right), \\ I & = \frac{I}{7} + \frac{9Ml^2}{2}, \\ \frac{6I}{7} & = \frac{9Ml^2}{2}, \\ I & = \frac{21Ml^2}{4}. \end{align*}

This seems incorrect? It feels wrong, comparing to a disk of radius $l/2$ which has moment of inertia $Ml^2/4$ it seems far too large.

It would also be nice if we could verify our answer numerically or otherwise. Any references are also appreciated.

Answer 1

I think that your $\frac{\sqrt{3}}{2}$ for the distance between hexagons center is not right... The distance from an hexagon center to an edge is $\frac{r\sqrt{3}}{2}$, thus the distance between two hexagons of radius $\frac{l}{2\sqrt{7}}$ that touch by an edge should be: $$d = l\sqrt{\frac{3}{28}}$$

Now, if we take back your computation: $I = \frac{I}{49} + 6 \left(\frac{I}{49} + \frac{3Ml^2}{28}\right)$

This gives us : $I = \frac{3}{4} M l^2$, which may still not be the right answer.

It would be nice to compare this value to numerical methods, I'll look into it.

e/ I ran some numerical simulation, unfortunately it does not seem to confirm the above result.

The code.

How I did it:

• Starting from the code linked in this page, I generated the all points composing the outer shape of the gosper island.
• Then, I trimmed the generating points to remove duplicates
• I approximate the Gosper island as being star-shaped (This is not perfectly true, at least for $n=5$). Then its inertia is the sum of the inertia of the triangles composed of the origin and two consecutive points. Note that to get the actual inertia, one has to divide by the shape's area (Because when evaluating the triangle's inertia, we consider it has a surfacic mass of 1.). All triangle related formulas are available on Wolfram Alpha.

The results show that indeed the inertia is proportional to $l^2$, but its ratio to the value conjectured above is not 1, but a constant close to $\frac{4}{7}$: $$ I_{gosper} \approx 0.568582263418 \frac{3}{4} M l^2$$

Unfortunately, it seems that this error is not related to the star-shaped approximation: I ran another experiment, this time using the Seidel program from the University of North Carolina at Chapel Hill. It allowed me to find a triangulation of the inner area of the Gosper island. Using another (similar) code I could check that the computation for a radius of 1. does yield the same ration between expected inertia (0.75) and the actual inertia (0.42856647032), with a similar ratio of 0.571421960426. Note that this inertia is very close to $\frac{3}{7}$, (best fractional approximation with a denominator inferior to fifteen thousand).

Actually, I had forgotten that the characteristic dimension is not the diameter, but the radius, thus the ratio is 0.142855490107, very close to $\frac{1}{7}$.

Using this method for a Koch snowflake yields pretty correct results: for a snowflake of radius $r \approx 1.44$ (I forgot to scale the step size properly) I get an inertia of $I_{koch} \approx 0.736036125705$ while the one given by $Ml^2/11 \approx 0.7435999999999999$

e/ I found the error: The mass of a "small" Gosper island is not $M$, but $\frac{M}{7}$, thus the missing factor 7. This is due to the fact that we make the assumption of a uniform density Gosper Island, thus its mass is proportional to its area.

We can rewrite our original equation: $$ I_{edge} = I_{center} + \frac{M}{7}d^2\\ d = l \sqrt{\frac{3}{28}}$$

Which gives us: $$ I = \frac{I}{49} + 6 \left( \frac{I}{49} + \frac{3Ml^2}{7\cdot 28}\right)$$

And finally:

$$I = \frac{3Ml^2}{28}$$

Answer 2

Yes, the distance between those hexagon-like shapes in a hexagonal lattice is the same as the distance between centres of hexagons of the same area in a hexagonal lattice.

The reason is that "in the long run" the area per mesh must be the same. That is, a sufficiently large circular disk contains both Gosper islands and hexagons in a number approximately equal to area of the disk dividied by area of the shape (with an error in the order of magnitude proportional to the cirumference of the disk).

Answer 3

The area inside the hexagon is made of one whole island and exactly six thirds, by symmetry.

Hence for an island of unit area, the distance between centers is such that

$$3\frac{\sqrt3}2d^2=3,$$

$$d=\sqrt{\frac2{\sqrt3}}.$$

---

To compute the moment of inertia, we will work with the radius of gyration and for an island of unit area.

$$I=MR^2$$ where $M$ is the mass.

For the assembly in the figure, enlarging by the factor $\sqrt7$ and using the axis theorem,

$$7M7R^2=49I=I+6(I+Md^2),$$

giving

$$R=\frac d{\sqrt7}=\sqrt{\frac{2}{7\sqrt3}}=0.406149258\cdots$$

This compares to the radius of gyration of a unit area disk,

$$R'=\frac1{\sqrt{2\pi}}=0.398942280\cdots$$

and that of a unit area hexagon,

$$R''=\sqrt{\frac{10}{36\sqrt3}}=0.400468569\cdots$$