How do we know the ratio between circumference and diameter is the same for all circles?

Question

The number $\pi$ is defined as the ratio between the circumeference and diameter of a circle. How do we know the value $\pi$ is correct for every circle? How do we truly know the value is the same for every circle?

How do we know that $\pi = {C\over d}$ for any circle? Is there a proof that states the following: Given any circle we know that $\pi = {C\over d}$. Doesn't such a statement require a proof considering $\pi$ is used so widely on problems involved with circles, spheres, etc. How do we truly know that the value $\pi$ is correct for all circles?

Answer 1

This is not a very rigorous proof, but it is how I was taught the fact that the circumference of a circle is proportional to its radius.

Consider two concentric circles as in the diagram above. The radius of the smaller one is $r$, while that of the larger one, $R$; their circumferences are $c$ and $C$ respectively.

We draw two lines through the center to meet each circle, forming two triangles as shown. The ratio of their sides $r/R = r/R$, and they have a common angle $\alpha$, so they are similar. Thus $k/K = r/R$. Also note that if $\beta$ denotes the full (360 degree) angle of a circle, then $\beta/\alpha \cdot k \approx c$ and $\beta/\alpha \cdot K \approx C$.

We can say that $\frac{c}{C} \approx \frac{\beta/\alpha \cdot k}{\beta/\alpha \cdot K} = \frac{r}{R}$. As the angle $\alpha$ becomes smaller and smaller (tending towards zero, to make a limiting argument) the approximations $\beta/\alpha \cdot k \approx c$ and $\beta/\alpha \cdot K \approx C$ grow more accurate. In the limiting case -- and this is where the 'proof' is slightly nonrigorous -- we get that $\frac{c}{C} = \frac{r}{R}$.

Thus $c/r = C/R$ or equivalently $c/(2r) = C/(2R)$: the circumference divided by the diameter is always a constant for any two circles since any two circles can be made concentric by a trivial translation. We call this magic constant $\pi$.

Answer 2

Here is a rigorous proof.

First, we need a definition for the distance of two points along a section of a curve. This is called arc length and is defined as the limit of the sum of line-segments of the curve.

The proper definition may be found here. Using this definition, it follows that the arc length $s$ between two points $a$ and $b$ for a continuously differentiable function $f: \mathbb{R} \to \mathbb{R}$ may be calculated by

$$ s = \int_a^b \sqrt{1 + f'(x)^2} dx$$

Lets compute with this formula the arc length $s$ of the upper half of a circle with radius $r$. Using Pythagoras the function describing the upper circle goes from $-r$ to $r$ and is defined as $f(x) = \sqrt{r^2-x^2}$

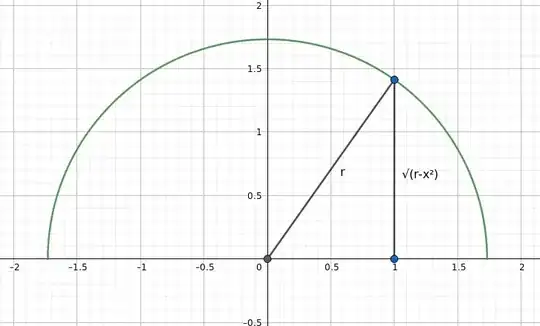
Also by the chain-rule we have

$$ f'(x)= \frac{-x}{\sqrt{r^2-x^2}}$$

thus

$$ s = \int_{-r}^r \sqrt{1 + \frac{x^2}{r^2-x^2} } dx = \int_{-r}^r \sqrt{ \frac{r^2}{r^2-x^2} } dx= \int_{-r}^r \sqrt{ \frac{1}{1-(x/r)^2} } dx$$

which is if you substitute* with $\phi(x)=rx$:

$$ s =r \int_{-1}^1 \frac{1}{\sqrt{1-x^2}}dx $$

Now $$\int_{-1}^1 \frac{1}{\sqrt{1-(x)^2}} dx:= c_0$$ is clearly a constant that does not depend on the circle (it does not depend on $r$). Since $2s=C$ is the circumference and $2r =d$ is the diameter we have

$$\frac{C}{d} = \frac{s}{r} = c_0$$ for any circle. Which shows, that the ratio between the circumference and diameter of any circle is always $c_0$. This constant is known by the symbol $\pi$.

*To be precise, the substitution rule is

$$ \int_{a}^b h(\phi(x)) \phi'(x) dx = \int_{\phi(a)}^{\phi(b)} h(u)du $$

in this case we have $$ h(x) = \sqrt{\frac{1}{1-(\frac{x}{r})^2} } \text{ and }\phi(x) = rx$$

Answer 3

To show that $\pi$ is constant we must show that given two circles of diameters $d_1$ and $d_2$ and circumferences $c_1$ and $c_2$, respectively, that $\frac{c_1}{d_1}=\frac{c_2}{d_2}$.

If $d_1=d_2$ then the two circles are congruent because one can be placed upon the other and they will line up. Without loss of generality we can assume $d_1\lt d_2$. Draw the circles concentrically. Then $d_2=kd_1$ for some $k$. If we can show that $c_1=kc_2$ then $\frac{c_2}{d_2}=\frac{kc_1}{kd_1}=\frac{c_1}{d_1}$ and we will be done.

Label the common center of the two circles $O$. Construct two rays emanating from $O$ outwards that divide each of the circles' circumferences into $n$ equal parts where $n\gt 2$. Label the points where the two rays intersect the inner circle $A$ and $B$ and the points where they intersect the outer circle $A'$ and $B'$. Choose the $A'$ so that it lies on the same ray as $A$.

Now consider the triangles $AOB$ and $A'OB'$. These two triangles are similar and moreover, the ratio $\frac{\overline {A'B'}}{\overline{AB}}=\frac{A'}{A}=\frac{\frac{d_2}{2}}{\frac{d_1}{2}}=\frac{d_2}{d_1}=\frac{kd_1}{d_1}=k$. Therefore, $\overline{A'B'}=k\overline{AB}$.

The perimeter of the regular $n$-gon inscribed inside the inner circle is given by $n$ copies of $\overline{AB}$ and the perimeter of the regular $n$-gon inscribed inside the outer circle is $n$ times the length of $\overline{A'B'}$.

Therefore, the perimeter of the inner $n$-gon is $n|\overline{AB}|$ and the perimeter of the outer $n$-gon is given by $n|\overline{A'B'}|=kn|\overline{AB}|$. The ratio of the two perimeters is $k$ and this is independent of $n$.

Taking $n$ arbitrarily large gives that the ratio of the two circumferences are also equal to $k$ and the result is proved.

Answer 4

Very interesting question. I reckon that any answer will have to do with what the perimeter is even defined as. If we take it as limit of n-glons, then it is easy to see that ratio of perimeters of polygons (at least $2n$-polygons) to their diameter is constant. Thus in limit, too, the ratio will remain constant.

Note: Early Greek mathematicians did have an idea of circles (and many other curved objects) as limits of polygons.

Answer 5

I don't know why you flat earthers believe that the ratio of circumference to diameter is pi. That is only a limiting case for very small circles. I checked on my globe, and found that, for example, a circle of diameter 12,000 miles has a circumference of approximately 24,000 miles. That is a ratio of 2, not pi.

Of course, even larger circles are possible whose diameters are more than halfway around the globe, and the limiting case is a diameter of 24,000 miles for a tiny circle that encloses all of earth except for a tiny area around the south pole with circumference close to zero. So the ratio can get as small as you like.

Answer 6

This is how I have always visualised this question. Think of an equilateral triangle, the ratio of its perimeter to the distance from the corner to the center is constant irregardless of the length of the side of the equilateral triangle. Now, replace this with a square. The ratio of its perimeter to the distance from the corner to the center is also constant irregardless of the length of the side of the square. By now, you'll probably guess what's next. Yup, its the pentagon. Same result. Hexagon, heptagon, octagon, nonagon, decagon, etc. Yes again, same result. A circle is just a polygon with equal infinite sides of infinitesimally small length. And naturally the ratio of its perimeter (circumference) to the distance from its corner to the center (radius) is also a constant irregardless of how big the circle is. Thus this ratio was defined as 2π. Hope this helps!

Answer 7

A more rigorous and complete answer is given by me and a co-author in a recent paper entitled "Why is it that the Ratio of Any Circle’s Circumference to its Diameter is a Constant?", to be published in the next issue of "College Mathematics Journal" (April/2022), see Taylor and Francis website. I'll post a link as soon as it is published online.