8

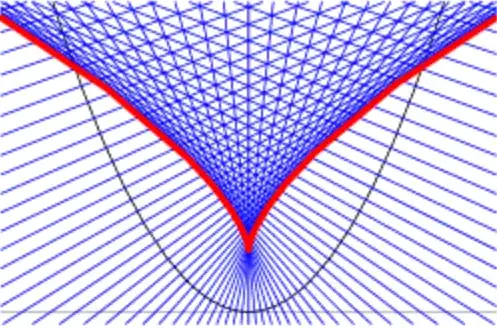
I know how to find a reflection with respect to one of the axis or with respect to the origin, but let's say I want to find the reflection with respect to a parabola, how do I do it? Let's say we have the standard $y = x^2$, in this case each point needs to be reflected by projecting them onto the parabola by finding the point whose tangent line at that point of the parabola and the line from the point to the parabola are perpendicular. Then the reflection would the point on the other side. So (0,1) goes to (0,-1). Is there a way to find a general formula?

I am thinking that since the parabola is $y = x^2$, I should be able to map the axis y=0 to $y=x^2$, and then any pair of points (x,y) and (x,-y), symmetric with respect to the y axis, would remain symmetric with respect to the parabola. But what is this mapping?

EDIT: Is there a better way to define this reflection by only considering the x>0 half-plane, and adding the constraint that the reflected points must still be in the x>0 half-plane? Similarly to how the area under the y=0 axis for x>0 is reflected into the area over y=0 and x>0 for a reflection about the y=0 axis, I also would like the reflection for the area x>0 under the parabola to be reflected in a point x>0 inside the parabola. I am looking at a deformation of the plane that takes the y=0 line onto the parabola and drags all the points with it. Symmetric points after the deformation should match those before the deformation.

user
  • 1,123
  • The "interior" of a reflecting parabolic surface is often used to focus light (or sound) traveling from a long distance (and thus having nearly parallel paths to the axis) onto the focus of the (longitudinal) parabolic cross-section. If your Question is about the reflection of such paths as they reach the parabola, I think the wording would improve by emphasizing this "path" reflection (rather than "point" reflection). – hardmath Apr 28 '16 at 19:47
  • You could reflect in the tangent line of the closest point on the curve. If you don't want to do that you could reflect in some other point, but then it is not as obvious to me what that should mean. I just realized I probably meant the other kind of reflection than hardmath wrote about, i.e. if you want the image on the "other side of the curve". – mathreadler Apr 28 '16 at 19:51
  • Consider looking into Schwarzian reflection and the Schwarzian derivative of complex analysis... – QuantumFool Apr 29 '16 at 03:08

2 Answers2

13

The problem here is that the normal lines (the lines perpendicular to the tangent lines) to a parabola are not parallel, as they are for straight lines.

That means that a given point in the plane can be on more than one normal line simultaneously. The question is then: which normal line do you use to reflect?

The evolute, i.e. the envelope of normal lines, is the key here. In the case of $y=x^2$, the evolute is parametrised by $x=4t^3$ and $y=3t^2+\frac{1}{2}$. This curve gives a cusp. The points "inside" the cusp lie on three different normal lines. The points outside the cusp lie on a single normal line. The points on the cusp lie on two normal lines.

The following picture is from MathWorld and show normal lines to a parabola. Notice how points inside the cusp lie on three normals, points on the cusp lie on two normals, and points outside the cusp lie on one normal.

enter image description here

Fly by Night
  • 32,272
  • 1
    That's a curious way to generate a hex grid. Maybe any region for a curve having three such lines passing through could generate some hex grid. – mathreadler Apr 28 '16 at 20:28
  • 2
    I suppose we could use "closest point on the parabola" to find a unique image for every point (except for some points on the axis of the parabola), but this figure shows that the mapping is not one-to-one, and with a little thought it seems clear that it also is not onto--there is a large region below the parabola consisting of points that will not be the reflected image of any point. – David K Apr 28 '16 at 20:36
  • 1
    I don't see clearly how there could be such a large region below though. My intuition tells me that by continouity all points should have at least one line passing through for this particular curve. – mathreadler Apr 28 '16 at 21:10
  • 1
    @mathreadler You are correct. Deciding if a normal line passes through a point in the plane reduces to solving a single variable cubic equation. These always have at least one real root, i.e. every point has at least one normal passing through it. The evolute corresponds to the cubics with a repeated root (usually one simple and one double). The inside of the evolute corresponds to three simple roots. The cusp point itself corresponds to a triple root. – Fly by Night Apr 28 '16 at 21:17
  • @mathreadler: David is saying there is a region that is not the reflected image of any point (if reflection is defined using the closest point on the parabola). I agree with him. – user21820 Apr 29 '16 at 04:17
  • Ah okay, then if it is defined by closest point I agree. – mathreadler Apr 29 '16 at 08:28
4

I will add the brutal (force) numerical solution ( in MATLAB).

% Author - Chenguang Zhang
% create a circle to be mirrored
theta = linspace(0, 2*pi, 50);
radius = 0.2;
as = 0.0 + radius * cos(theta);
bs = 0.5 + radius * sin(theta);


figure(1)
hold on
xx = linspace(-3,3,101);
plot(xx, xx.*xx, 'b-', 'LineWidth', 2)
plot(as, bs, 'ro')

for ii = 1:length(theta)
    a = as(ii);
    b = bs(ii);
    troots = roots([1 0 0.5-b -0.5*a]);
    for i = 1:length(troots)
        t = troots(i);
        if(imag(t) ~= 0)
            continue;
        end
        x = t;
        y = t*t;
        p_reflect = [2*x - a, 2*y - b];
        plot(p_reflect(1), p_reflect(2), 'bo')
    end
end

An image from multiple runs with different circles location and shape is below. circle mirrored by parabola

Taozi
  • 2,643
  • 13
  • 19
  • what is the matlab picture of the reflection for the line y=x? – user Apr 29 '16 at 06:29
  • @user I can't post image in comment, you can change the code. Just change as and bs to be x and y of the line. – Taozi Apr 29 '16 at 07:08