1

there is an exact same question, with an answer, but I don't get it and I can't comment. existing question

I figured out, that

$$S = \int 2\pi r dr$$

where

$$r = R/H dh$$

so that

$$S = 2\pi \frac{R}{H} \int h dh$$

but this yields

$$\pi rh$$
instead of $$\pi rs$$ where s is the "length" of the side of a cone

In comments by the existing answer there is written:

You can't integrate circumferences to get a surface area for the same reason you can't integrate points to get a length.

But I had thought (and think) that:

You can integrate circumferences to get a surface area for the same reason you can integrate surface to get a volume.

So what's the problem?

Community
  • 1
Adam
  • 159

1 Answers1

0

There seem to be three issues here. The first is the integral you so wrongly attempted: by proportion, $$\frac rR=\frac hH$$ So $$r=\frac RHh$$ and $$dr=\frac RHdh$$ Then $$\bar S=\int_0^R2\pi r\,dr=\int_0^H2\pi\frac RHh\cdot\frac RHdh=\pi R^2$$ so the situation is even worse! Now there's the issue about integrating lengths to get an area like integrating areas to get a length. You can't always do these things. Let me give an illustration: Figure 1

Now, in figure 1 we would like the area of the blue sector of an annulus from $r=R_1$ to $r=R_2$ and from $\theta=\theta_1$ to $\theta=\theta_2$. So I start with a line from $(x,y)=(R_1\cos\theta,R_1\sin\theta)$ to $(x,y)=(R_2\cos\theta,R_2\sin\theta)$ and want to add up the red area between that line and the line from $(x,y)=(R_1\cos(\theta+d\theta),R_1\sin(\theta+d\theta))$ to $(x,y)=(R_2\cos(\theta+d\theta),R_2\sin(\theta+d\theta))$.

Now, one might think that one should multiply the length of the first line by the width of the red area and add up over all potential red areas, but there is a problem in that the red area doesn't have uniform width. So in practice you would have to find the average width and multiply by that. The same issue arises in adding up areas to get volumes, but you have only been exposed thus far to problems where the width of the zone between the areas is uniform.

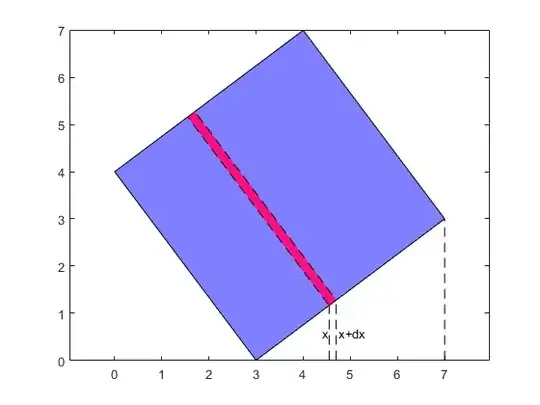
The last issue is that even when the width of the areas is uniform you have to compute that width from the variable of integration when setting up the integral. Another illustration: figure 2

In figure 2, we want to compute the area of the blue square with corners at $(3,0)$, $(7,3)$, $(4,7)$, and $(0,4)$. So we'll start from $x=3$ up to $x=7$ and draw lines from the $x$-axis at $(x,0)$ and $(x+dx,0)$ up to the square and the draw a red rectangle from where these lines meet the square. The length of the red rectangle is a side of the square, $5$. But the width $dw$ is not $dx$. From similar triangles we could show that $$\frac{dw}5=\frac{dx}4$$ so $$dw=\frac54dx$$ Now we can find the area of the blue square: $$A=\int h\,dw=\int_3^75\cdot\frac54dx=\left.\frac{25}4x\right|_3^7=25$$ Back the the area of a cone: the distance between a circumference at $(r,h)$ and $(r+dr,h+dh)$ is not $dr$ but $$ds=\sqrt{(dr)^2+(dh)^2}=\sqrt{1+\left(\frac HR\right)^2}dr$$ So you need $$A=\int2\pi r\,ds=\int_0^R2\pi r\sqrt{1+\left(\frac HR\right)^2}dr=\pi R\sqrt{R^2+H^2}$$

user5713492
  • 15,938
  • Thanks, I get all of that except when you go back to the cone part :D. I don't know what "dh" is and why it is H/R and not R/H. Maybe I have my graph turned 90 degrees. Could you please more explain this or provide a valid graph? – Adam Apr 17 '16 at 20:36
  • Those graphs are way too expensive for me to draw. On the surface of the cone, $$\frac hH=\frac rR$$ When $r$ goes from $r$ to $r+dr$, $h$ goes from $h$ to $h+dh$. Then $$\frac{h+dh}H=\frac{r+dr}R$$ so $$\frac{dh}H=\frac{dr}R$$ Then $$dh=\frac HRdr$$ The nearest distance between the circumferences at $(r,h)$ and $(r+dr,h+dh)$ is $$ds=\sqrt{(dr)^2+(dh)^2}=\sqrt{(dr)^2+\left(\frac HR\right)^2(dr)^2}=\sqrt{1+\left(\frac HR\right)^2}dr$$ – user5713492 Apr 17 '16 at 20:53
  • And does this mean you have to count the volume similarly except you use pi*r^2? – Adam Apr 19 '16 at 06:02
  • I'm not 100% sure what you're saying but my humble illustrations could be extended to $3$-d by imagining figure $1$ to be a piece sawed out of a (thick) pipe or figure $2$ to be extended out of the plane of the picture as a cube. In either case you have to make corrections if the sections the object is sliced up into aren't of uniform thickness or aren't crossed by the coordinate corresponding to the variable of integration at right angles. – user5713492 Apr 19 '16 at 16:51