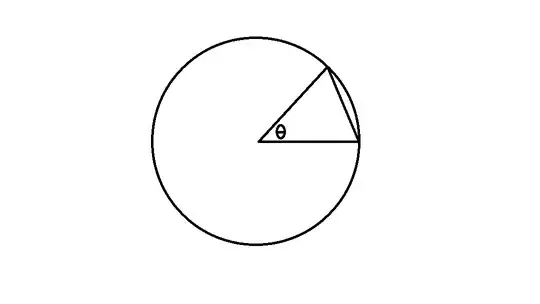
Is there a good way to show that $\frac{\sin(x)}{x}$ is bounded above by $1$?
We can see visually that $\frac{\sin(x)}{x}$ is bounded above by $1$ because the tallest hump is at the origin and $\lim_{x \to 0} \frac{\sin(x)}{x}=1$. But is there a way to prove this rigorously? Preferably without expanding $\sin(x)$ into a Taylor series, unless Taylor series is the only way.
Clearly, $|\sin(x)|\leq |x|$ when $|x|>1$. For $|x|\leq 1$, you can use the mean value theorem to show that $x=0$ is the only solution to $\sin x=x$. Thus, $\sin x<x$ for $x>0$ and $\sin(x)>x $ for $x<0$. This implies that $$\left|\frac{\sin(x)}{x}\right|\leq 1.$$
Consider this image of the unit circle where the area of the triangle is $\frac{1}{2}\sin(\theta)$ and the area of the circle sector is $\frac{1}{2}\theta$.
You can see that $\frac{1}{2}\sin(\theta) \le \frac{1}{2}\theta.$
Use $\sin'(x) =\cos(x) $, and $\cos(x) \le 1$ to get, for $x \ge 0$, $\sin(x) =\int_0^x \cos(t)dt \le \int_0^x 1dt =x $.
L'Hopital's rule works: $$ \lim_{x \to 0}\frac{\sin(x)}{\ x} $$ Becomes $$ \lim_{x \to 0}\frac{\cos(x)}{\ 1} $$ Evaluating to $$ 1 $$
It may not be as rigorous as you want though.
