Is there a deeper meaning to the identity ${{\sin x}\over x} = \prod_{k=1}^{\infty} \cos\left({x\over{2^k}}\right)$?

Question

Is there any deeper meaning to trigonometric identity $${{\sin x}\over x} = \prod_{k=1}^{\infty} \cos\left({x\over{2^k}}\right)$$ beyond it corresponding to characteristic functions of i.i.d. random variables?

Answer 1

I give 2 proofs, showing that there is something in this formula, beyond its intrinsic beauty.

First proof:

Let us consider the formula under the form:

$$\frac{\sin \pi x}{\pi x} = \prod_{k=1}^{\infty}\cos{\frac{\pi x}{2^k}}= \lim_{n \rightarrow \infty}{\prod_{k=1}^{n}\cos{\frac{\pi x}{2^k}}}$$

Its Fourier Transform (using Euler formula $\cos(a)=\frac{1}{2}(e^{ia}+e^{-ia}))$ and the fact that a product is transformed into a convolution, is:

$$\mathbb{1}_{[-\frac{1}{2},\frac{1}{2}]}(u) = \lim_{n \rightarrow \infty}{{\Huge \ast}_{k=1}^{n}\frac{1}{2}\left(\delta(u+\frac{k}{2^{k+1}})+\delta(u-\frac{k}{2^{k+1}})\right)} \ \ \ (*)$$

Now, let us expand the convolution product ${\Huge \ast}_{k=1}^{n}$ on the RHS, in the particular case $n=3$ in order to understand what is going on, i.e.,

(using property $\delta(u-a)*\delta(u-b)=\delta(u-(a+b))$):

$$\frac{1}{8}\left(\delta(u+\frac{1}{4})+\delta(u-\frac{1}{4})\right)*\left(\delta(u+\frac{1}{8})+\delta(u-\frac{1}{8})\right)*\left(\delta(u+\frac{1}{16})+\delta(u-\frac{1}{16})\right)$$

$$=\frac{1}{8}\left(\delta(u+\frac{1}{4}+\frac{1}{8}+\frac{1}{16})+\delta(u+\frac{1}{4}+\frac{1}{8}-\frac{1}{16})+\cdots+\delta(u-\frac{1}{4}-\frac{1}{8}-\frac{1}{16})\right)$$

$$=\frac{1}{8}\left(\delta(u+\frac{7}{16})+\delta(u+\frac{5}{16})+\cdots+\delta(u-\frac{7}{16}))\right)$$

The general case being:

$$\prod_{k=1}^{n}\frac{1}{2}\left(\delta(u+\frac{k}{2^{k+1}})+\delta(u-\frac{k}{2^{k+1}})\right)=\frac{1}{2^n}\sum_{k=-2^{n}+1}^{k=2^{n}-1}\delta(u+\frac{k}{2^{n+1}})$$

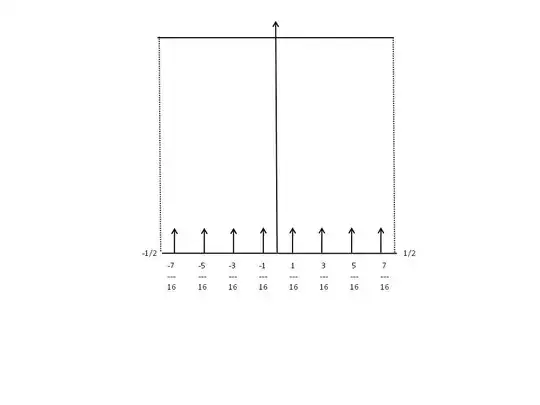
Explanation: each term obtained in the development of the product gives rise to a number that can be (up to factorization by $1/2$) written as the base-2 decomposition of a number of the form $\dfrac{N}{2^{n+1}}$, all numbers of this form being represented exactly once. This is why we obtain a regular spacing.

(Nice) interpretation :

• Intuitively, the uniformly spread "mass" on interval $[-\frac{1}{2},\frac{1}{2}]$ is placed into $2^n$ "Dirac bins".

• In more probabilistic (or "measure theory") and rigorous terms, the transformed formula expresses a convergence of a regularly spaced discrete uniform distribution to its continuous counterpart.

The figure below illustrates this kind of equivalence between the continuous measure represented by the characteristic function of $[-1/2,1/2]$ and the "Dirac forest" made (in our particular case) of 8 regularly spaced "Dirac trees" of height=mass 1/8 each.

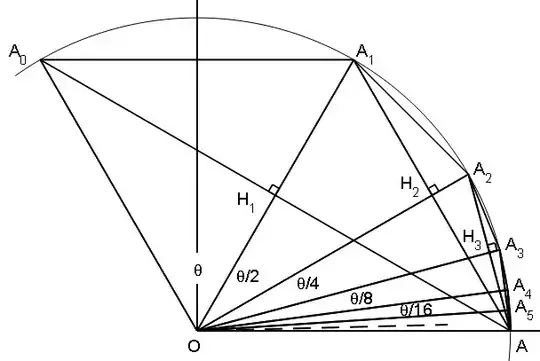
Edit: A second proof using a very different, entirely geometrical, interpretation:

Let us consider the figure below with $A_k(\cos\left(\dfrac{\theta}{2^{k-1}}\right),\sin\left(\dfrac{\theta}{2^{k-1}}\right))$ and $H_k=AA_k \cap OA_k$.

Let us establish relationship

$$AH_{k+1}=\dfrac{AH_k}{2 \cos\left(\dfrac{\theta}{2^{k}}\right)} \ \ \ (1)$$

In order to follow more easily, we will take the particular case $n=2$ WLOG:

Relationship $AH_{3}=\dfrac{AH_2}{2 \cos\left(\dfrac{\theta}{4}\right)}$ is the consequence of two facts:

• $AA_2=2 AH_3$ ($H_2$ is the foot of the altitude in isosceles triangle $AOA_1$) and

• $AH_2=AA_2 \cos\left(\dfrac{\theta}{4}\right) \ $ by inscribed angle theorem: (https://en.wikipedia.org/wiki/Inscribed_angle): the angle under which arc $A_1A_2$ is "seen" from $A$ is half the angle under which it is "seen" from the center $0$).

Thus, from (1),

$$AH_{n+1}=\dfrac{AH_1}{2^{n} \prod_{k=1}^{n}\cos\left(\dfrac{\theta}{2^{k}}\right)} \ \ \ (2)$$ But, if $n$ is large, $$AH_{n+1}=H_{n+1}A_{n}=sin\left(\dfrac{\theta}{2^{n}}\right)\approx \dfrac{\theta}{2^{n}} \ \ \ (3) $$

(classical approximation for small angles). Thus, taking into account that $AH_1=\sin \theta$, grouping (2) and (3) gives:

$$\dfrac{\sin \theta}{2^{n} \prod_{k=1}^{n}\cos\left(\dfrac{\theta}{2^{k}}\right)}\approx\dfrac{\theta}{2^{n}} \ \ \ (4)$$

After cancellation of $2^n$ in both sides, formula (4) is clearly a proof of the infinite product formula.

Note: A rigorous treatment would necessitate to replace the approximation argument by a limit argument, which is rather easy...