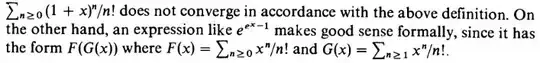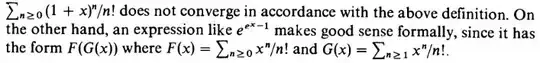There is a simple, natural notion of convergence that settles this and related matters, and it can be presented in a elementary way that requires no knowledge of topology. For example, see the discussion below (excerpted from Stanley's classic $ $ Enumerative Combinatorics I). $ $ In particular, the final paragraph shows how this applies to your problem of composition of formal power series.
Note $ $ Beware that there is widespread confusion between formal vs. analytic power series, and this often clouds discussion of this and related matters (as Rota often remarked, even some eminent mathematicians have published nonsense based on such confusion). For example, see this closely related question on products of formal power series (which was initially clouded by such confusion - see esp. the deleted answer and comments). It seems that - just as for polynomials - it proves difficult for some to shed analytic (function) bias and pass to purely algebraic (formal) abstraction.