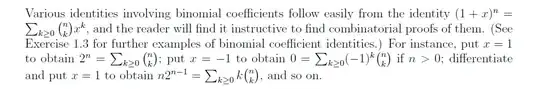0

In every source I've read about generating functions if $A(x)$ is a generating function, we treat $x$ as an indeterminate, in particular, it is treated as a placeholder. And if one goes on with what Wikipedia says about an indeterminate variable, https://en.wikipedia.org/wiki/Indeterminate_(variable), one can not treat $x$ as a number, for instance (i might be misunderstanding).

I am having the confusion about why in some cases we can assign a value to $x$. I'll appreciate if someone clarifies my misunderstanding.

Example, in Stanley's Enumerative Combinatorics he makes x=1 when trying to prove that $$n2^{n-1} = \sum_{k\geq0}k\binom{n}{k} $$

enter image description here

Sahan Manodya
  • 982
Mangostino
  • 525
  • 1
    I think you are misunderstanding the distinction between a "variable" and an "indeterminant", at least as "indeterminant" is being used in that wikipedia article. In that article, they are talking about very abstract "algebra" in which "X" is treated as an object in itself- not representing anything. In the algebra you (and I) are more familiar with the "variables" always represent a number of some kind. THAT is the sense in which we can set x= 1. – user247327 Sep 12 '21 at 17:27
  • 1
    In formal power series, one manipulates the indeterminates without regard for convergence of the series. Once you start plugging in numbers for $x$, you need to consider things like convergence, division by $0$ (like in $\frac{1}{1-x} = \sum_{k \ge 0} x^k$), etc., but otherwise the manipulations on the formal power series can still inform what happens when you plug in numbers for $x$. – angryavian Sep 12 '21 at 17:30
  • 1
    As a further clarification: With generating functions for fast-growing sequences, it may be that $A(x)$ and $B(x)$ do not converge for any $x$, except for $x=0$. If additionally $A(0)=B(0)$, then there is no distinction between $A$ and $B$ as (partial) functions over $\Bbb C$, but they can still be different because they have different coefficients - of which we can only speak by not treating $x$ as a number. – Hagen von Eitzen Sep 12 '21 at 17:31
  • See also here on convergence notions for formal power series. – Bill Dubuque Oct 30 '21 at 19:42

1 Answers1

2

Every formal power series $f(x)=\sum_{n\ge 0} a_nx^n$ has a radius of convergence, $R$, which is can be found via $$ 1/R = \limsup_{n\to\infty} \sqrt[n]{a_n}. $$ If the $\limsup$ is zero, then $R$ is defined to be $\infty$. Now, the rule is this:

You are allowed to substitute a particular number $x_0$ for $x$ in $f(x)$ as long as $|x_0|<R$.

In particular, if $f(x)$ is a polynomial, then the $R$ is always $\infty$, so you can substitute anything for $x$. This is the case for the Stanley example in your post, the polynomial being $n(1+x)^{n-1}$.

Mike Earnest
  • 75,930