As I am no mathematician, I have been struggling to find an equation to accurately predict points spaced along a curve separated by distance d. Given two points, assume a string with a length equal to 125% of the distance between the two points. If the string is "hooked" at its ends to the two points, what is the equation to find a third point p at some distance along the downward arc created by the hanging string?
Asked
Active
Viewed 3,278 times
2
-
Just asking: Do you know calculus? Also, are there simplifying conditions, e.g., the two points are at the same height? – Andrew D. Hwang Jan 03 '16 at 23:52
-
1I do know calculus, and have no qualms using it in a solution to this problem. Also, there are no simplifying conditions as this question is rather theoretical – Nathan Jan 04 '16 at 00:31
-
2Without loss of generality you can treat this as a 2D problem in the vertical plane containing the two points. Wikipedia provides formulas relating $x$ and $y$ coordinates to the arc length of the catenary, which you might be able to invert. – Jan 04 '16 at 00:45
2 Answers
1
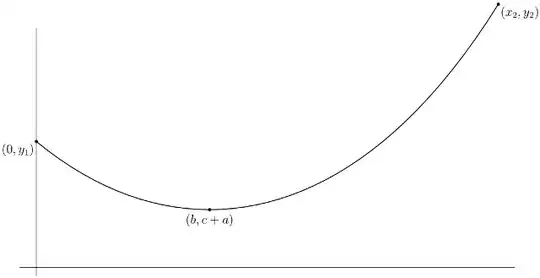
Call your known points $(0, y_{1})$ and $(x_{2}, y_{2})$. There exist constants $a$, $b$, and $c$ such that the desired catenary has equation $$ y = c + a\cosh \frac{x - b}{a}. \tag{1} $$ (This is the standard catenary of Wikipedia translated horizontally by $b$ and vertically by $c$.)
The arc length element of the graph is easily checked to be $$ ds = \cosh \frac{x - b}{a}\, dx. \tag{2} $$ The arc length from $(0, y_{1})$ to a general point $(x, y)$ with $0 \leq x \leq x_{2}$ is therefore $$ \ell(x) = \int_{0}^{x} \cosh \frac{t - b}{a}\, dt = a\left[\sinh \frac{x - b}{a} + \sinh \frac{b}{a}\right]. \tag{3} $$
Since the points $(0, y_{1})$ and $(x_{2}, y_{2})$ lie on the curve (1), you have $$ \left. \begin{aligned} y_{1} &= c + a \cosh \frac{b}{a}, \\ y_{2} &= c + a \cosh \frac{x_{2} - b}{a}. \end{aligned} \right\} \tag{4} $$ Since the arc length of the catenary is $125$% of the straight-line distance between the points $(0, y_{1})$ and $(x_{2}, y_{2})$, (3) gives $$ 1.25\sqrt{x_{2}^{2} + (y_{2} - y_{1})^{2}} = a\left[\sinh \frac{x_{2} - b}{a} + \sinh \frac{b}{a}\right]. \tag{5} $$
Equations (4) and (5) allow you to express $a$ and $b$ in terms of $x_{2}$, $y_{1}$, and $y_{2}$ (in principle; haven't tried to solve analytically in practice). Equation (3), which is easily solved for $x$ in terms of the distance to the point $p = (x, y)$ then gives the desired information.
Andrew D. Hwang
- 78,195
0
The difficult part of fitting a catenary of a specified length between two specified points is solving $y = \dfrac{\sinh(x)}{x} $ for $x$ in terms of $y$.
This can only be done numerically; there is no analytic solution.
Here is question with answers that tell you how:
marty cohen
- 107,799