I have the coordinates of one extreme point $D=(0,y_D)$, two lines $y = m_ix + y_D$ for $i\in \{ A,B \}$ intersecting the catenary at two point $A$ and $B$, and also in $D$. I know the length $L_{DA}$ of the catenary from $D$ to $A$, $L_{AB}$ from $A$ to $B$ and the overall length $L_{DE}$ from $D$ to $E$. I want to find the coordinates of the second extreme point $E$, as per the linked picture ($L = L_{AB}$).
My understanding is that given these conditions (one point, two intersections and a known distance between the intersections) the solution must be unique. My approach would be to find the equation of the catenary and then locate $E$, $L_{DE}$ away from the starting point $D$ along the curve.
I know that there is probably no analytical solution, as this involves a transcendental function. The equations I derived read as follows:
The shape of the catenary is expressed as $$y = c + a \cosh\left(\frac{x-b}{a}\right),$$
where $a,b,c$ are unknown. Three lengths are known
$$ L_{AB} = \int_{x_A}^{x_B} \cosh\left(\frac{t-b}{a}\right)dt = a\left[\sinh\left(\frac{x_B -b}{a}\right) - \sinh\left(\frac{x_A -b}{a}\right)\right] $$ $$ L_{DA} = \ldots = a\left[\sinh\left(\frac{x_A -b}{a}\right) - \sinh\left(\frac{-b}{a}\right)\right],$$ $$ L_{DE} = \ldots = a\left[\sinh\left(\frac{x_E -b}{a}\right) - \sinh\left(\frac{-b}{a}\right)\right],$$ and the two lines intersect the catenary $$y_A = c + a \cosh\left(\frac{x_A-b}{a}\right) = m_A x_A + y_D$$ $$y_B = c + a \cosh\left(\frac{x_B-b}{a}\right) = m_B x_B + y_D$$
I have looked at similar problems, such as Finding points along a catenary curve, but I do not know how to reduce this problem to that one. It seems to me the two coincide, once the coordinates $(x_A,y_A)$ or $(x_B, y_B)$ have been fixed. Is it possible to obtain a similar solution (i.e. analytically driven, but for the solution of the transcendental equation) or an algorithm to approximate the coordinates of $E$?
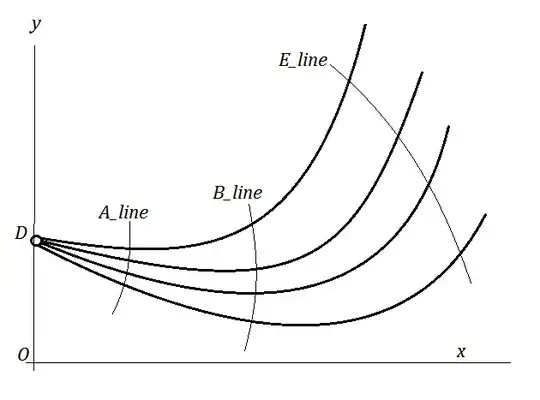
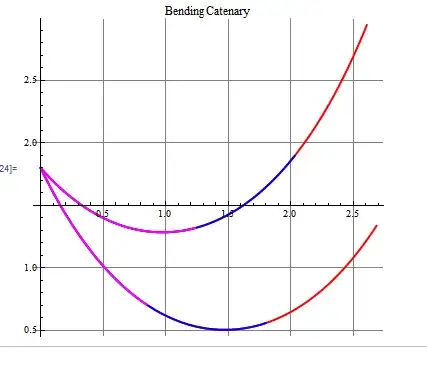
It seems that this solutions is really not robust though: many local minima exist, i.e. there are many catenaries that cross 2 lines forming 2 crossings with a certain distance $L$ or similar.
– Michele Bolognini May 31 '22 at 08:40