22

How can I solve the recurrence relation $T(n) = 2T(n/2) + n\log n$? It almost matches the Master Theorem except for the $n\log n$ part.

Arturo Magidin
  • 398,050
cody
  • 753

2 Answers2

18

Let us take $n = 2^m$. Then we have the recurrence $$T(2^m) = 2T(2^{m-1}) + 2^m \log_2(2^m) = 2T(2^{m-1}) + m 2^m$$ Calling $T(2^m)$ as $f(m)$, we get that \begin{align} f(m) & = 2 f(m-1) + m 2^m\\ & = 2(2f(m-2) + (m-1)2^{m-1}) + m2^m\\ & = 4f(m-2) + (m-1)2^m + m2^m\\ & = 4(2f(m-3) +(m-2)2^{m-2}) + (m-1)2^m + m2^m\\ & = 8f(m-3) +(m-2)2^m + (m-1)2^m + m2^m\\ \end{align} Proceeding on these lines, we get that \begin{align} f(m) &= 2^m f(0) + 2^m (1+2+3+\cdots+m) = 2^m f(0) + \dfrac{m(m+1)}{2}2^m\\ & = 2^m f(0) + m(m+1)2^{m-1} \end{align} Hence, $T(n) = n T(1) + n \left(\dfrac{\log_2(n) (1+\log_2(n))}{2} \right) = \mathcal{\Theta}(n \log^2 n)$.

  • Thank you. But if $T(2^m) = f(m)$, then isn't $T(2^{m-1}) = f(m/2)$ ? How do you get $f(m-1)$? – cody Jun 18 '12 at 01:31
  • 1
    @cody $T(2^m) = f(m)$. Now replace $m$ by $m-1$, we then get $T(2^{m-1}) = f(m-1)$. –  Jun 18 '12 at 01:41
  • I see. Thank you. So the trick to these recurrence relation is to transform them from the T(.) form to one of the summation series, right? – cody Jun 18 '12 at 02:01
  • ... and then prove by induction that the closed form is correct. – Raphael Jun 18 '12 at 18:26
  • @cody Yes. and as Raphael points out use induction/recursion. –  Jun 18 '12 at 18:28
1

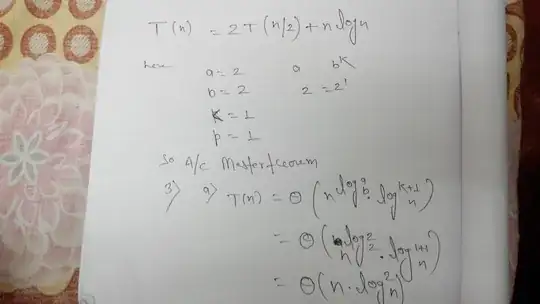
enter image description hereenter image description herethe given problem is best fit on master theorem

Naveen Kumar
  • 59
  • 1
    You just wrote the formulas, how is this an answer? And this problem isn't satisfied by the master theorem, so that's wrong too. – Mercury Oct 08 '20 at 16:29