7

Update: Updated the title now that I've observed that we can use math in the title. I've also gone thru and removed dots. The tool expresses quantification using dots like this $\forall x.P(x)$ rather than $\forall x P(x)$. I originally used these dots in my post as well.

I'm going through all of the proofs in The Incredible Proof Machine and need a hint for one of the proofs. (The Incredible Proof Machine is an online graphical proof tool.)

Given: $(\forall x P(x)) \to A $
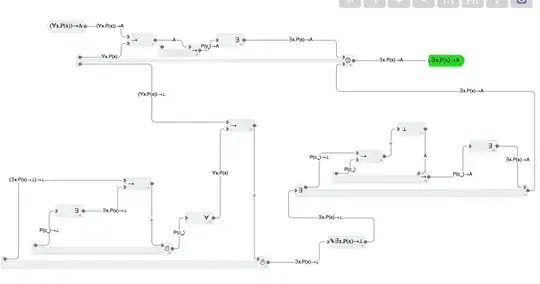
Prove: $\exists x (P(x) \to A )$

It seems like a trivial proof and here's my hand-waving attempt: There are two cases to consider:

  1. $\forall(x) P(x)$: In this case its trivial to prove the conclusion since we can prove $A$.
  2. $\neg \forall(x) P(x) $ In this case it must be that there exists some $c$ such that $ \neg P(c)$. Therefore trivially, $P(c) \to A$ and therefore $\exists x (P(x) \to A)$.

However, I get stuck trying to prove it using the actual logic connectors available in the tool. I'm not able to use the same approach in the second case of my case analysis (or at least I'm not sure how). This is my attempt:

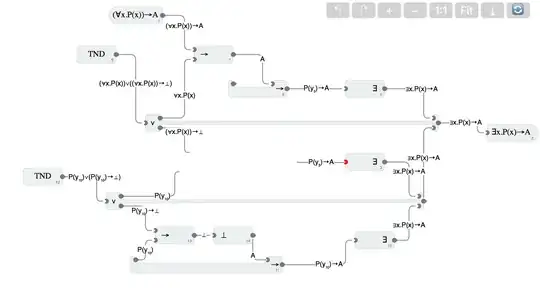
Proof Image

If you look right in the middle of the diagram you'll see there are no connections (and a small red dot indicating an error). This approach doesn't seem to lead anywhere.

I'm using two instances of TND to do case analysis. The first case is as described above. But I don't know how to handle the second case, so I used a TND in the second case to generate two sub-cases: $P(y_{10}) \vee (P(y_{10}) \to \bot)$. The second case of this TND is again trivial, but the first case doesn't lead anywhere.

In the middle of the proof I have two facts $P(y_{10})$ and $(\forall x P(X)) \to \bot$. These two facts don't seem like they can lead to the conclusion.

I'm looking for a hint of an approach to try to solve this proof.

Michael Welch
  • 288
  • I'm wondering if there is a way to use the universal introduction rule to transfer P(y10) into $\forall x.P(x)$. No attempt I tried worked. If it did work, then we could prove $\bot$ and therefore prove the conclusion. – Michael Welch Dec 14 '15 at 22:52
  • This is a question for the implementers or user community of the software. – Rob Arthan Dec 14 '15 at 23:05
  • 1
    I'm voting to close this question as off-topic because MSE is an inappropriate forum for help in using a new online resource. – Rob Arthan Dec 14 '15 at 23:08
  • 3
    I appreciate the concern. However I feel my question is not about the tool, it's about the proof. If you look at the tool, it's using a set of standard logic rules. These rules should apply no matter what tool you are using. If I determine there is a bug in the system that prevents me from solving the proof, that would be a question for the tool owner. – Michael Welch Dec 14 '15 at 23:22
  • I could just as easily remove the image and any mention of the tool and rephrase my question using just standard logic rules, however it would be more difficult for me to do so. – Michael Welch Dec 14 '15 at 23:24
  • I appreciate your point, but I think it is down to the implementers of this tool to document the rules they have implemented and explain why they believe the rules are adequate. – Rob Arthan Dec 14 '15 at 23:35
  • I did ask a question of the implementor. It was on his GitHub project for his tool. It was originally a question about the rules involving quantification and evolved into asking for a hint. I have no reason to believe the rules are not adequate to solve the proof. Therefore, I thought a Q&A site was a more appropriate place to ask a question about the proof than the Issues section of a github project which ideally are more to report real issues. Perhaps I was wrong in my assessment. https://github.com/nomeata/incredible/issues/71 – Michael Welch Dec 15 '15 at 01:38
  • I thought tools were supposed to make things easier. – Michael Dec 15 '15 at 06:21
  • I don't know what the dot means in $(\forall x. P(x))\rightarrow A$ ("for all x something..."). However, I notice that if we substitute $A \equiv (\forall x . P(x))$, then the given info is trivial and likely would not be useful for proving the desired thing, unless the assumption in the statement to be proved is a subset of $A$. In other words, though I have no idea what the interpretation of your symbols mean, is it possible that you are trying to prove something which is actually false? – Michael Dec 15 '15 at 06:26
  • If we interpret your mysterious dots in such a way that the first statement says "If $P(x)$ is true for all $x$, then $A$ is true" and that the second statement says "If there is an $x$ for which $P(x)$ is true, then $A$ is true" then certainly the first statement does not always imply the second. – Michael Dec 15 '15 at 06:29
  • You might want to explain your (possibly erroneous?) conclusion in part 2 of your writing above "therefore, trivially $P(c)\rightarrow A$." If I am understanding your notation correctly, this is neither trivial nor true. – Michael Dec 15 '15 at 06:42
  • @Michael The placement of the parentheses differs between the assumption and the conclusion. While you interpret the assumption correctly, the conclusion states that "there exists an $x$ such that if $P(x)$ is true then $A$ is true". Regarding the "mysterious dots". They are, of course, not my dots. They are the dots used by the tool itself and I guess they didn't trouble me as much as they did you. I just assumed they were playing the same role as dots in a lambda expression such as $\lambda x. x$, that is as a separator. If there is further semantic meaning, I may have overlooked it. – Michael Welch Dec 15 '15 at 14:06
  • In my second case then it is true that "there exists an $x$ such that if $P(x)$ is true then $A$ is true". I picked that $x$ to be $c$. And since $P(c)$ is false the implication is trivially true. – Michael Welch Dec 15 '15 at 14:11
  • Let us continue this discussion in chat. – Michael Welch Dec 15 '15 at 14:13
  • I think I've seen this question before here on math.stackexchange... – skyking Dec 15 '15 at 14:53
  • It seems related to http://math.stackexchange.com/questions/1098053/proof-of-exists-xpx-rightarrow-forall-y-py?rq=1 – Michael Welch Dec 15 '15 at 14:54
  • @Michael I've attempted to make the hand-waving proof more precise in this question: http://math.stackexchange.com/questions/1577767/a-proof-of-forall-x-px-to-a-rightarrow-exists-x-px-to-a – Michael Welch Dec 16 '15 at 14:26
  • Non empty universe assumed. See http://math.stackexchange.com/questions/1577767/a-proof-of-forall-x-px-to-a-rightarrow-exists-x-px-to-a Also my proof is now complete. See the accepted answer. – Michael Welch Dec 18 '15 at 04:48
  • I don't know about your, ahem... "Incredible Proof Machine", but the problem might be more tractable in the form $$[\forall x :[U(x) \to P(x) ]\to A ]\to \exists x:[U(x) \land [P(x) \to A]]$$ where $U$ is the universe predicate so that we could then explicitly assume a non-empty universe $$\exists x: U(x)$$ You could then write the antecedent equivalently as $$\exists x:[U(x) \land \neg P(a)] \lor A$$ giving you two cases to consider. – Dan Christensen Dec 18 '15 at 05:00
  • @MichaelWelch I have a much simpler proof that uses this $U$ predicate if anyone is interested (a 24 line, formal proof). Sorry, I didn't make use of the "Incredible Proof Machine." – Dan Christensen Dec 18 '15 at 05:04

1 Answers1

3

For other interested parties, I did get some hints from the tool community. If you wish to review these they are on this issue at GitHub

UPDATE: I finally finished the proof. The key to success was figuring out (with help) how to prove the identity $\neg \forall x P(x) \Rightarrow \exists x (\neg P(x))$. That identity was not built into the tool and can be a little tricky/cumbersome to prove from axioms. If you attempt the proof using the tool, learn how to create custom blocks like "proof by contradiction" and "case analysis". Otherwise the proof gets very messy. Here's the finished proof (still a little messy).

The blocks with the snowmen on them are "proof by contradiction". The block with baseball is case analysis.

Finished Proof

Michael Welch
  • 288
  • You really ought to be able to easily switch quantifiers. Is this a new program? My own DC Proof 2.0 has been around for years. I never would have released it without being able to switch quantifiers. Visit my website at http//www.dcproof.com – Dan Christensen Dec 18 '15 at 06:10