1

I'm trying to solve Burgers equation $(\rho_{t} + \rho \rho_{x} = 0$), interpreted as a conservation law for $\int \rho dx$, with

$$\rho (x_{0} ,0) = \begin{cases} 0 \quad & x_{0} \leq 0 \\ x \quad & 0 \leq x_{0} \leq 1 \\ 0 \quad & x_{0} > 1\end{cases}$$

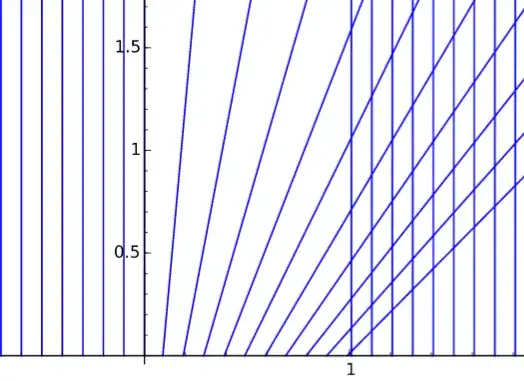
I'm thinking that I should use the method of characteristics, but I'm having problems treating the movement of the shock. It's obvious that the solution for $x<0$ is $0$. When $x$ is between $0 - 1 $
$$\dfrac{dx}{dt}=x \rightarrow \dfrac{dx}{x} = dt \rightarrow \ln(x) = t +c \rightarrow x= Ae^{t}$$
Applying the boundary conditions for $t=0$, first, solve for the constant (characteristic equation?) $A=xe^{-t}$, and I know that $\rho(x_{0},0) = x$, so $A=x_{0} e^{0}=x$. Therefore $A==x$, and $\rho(x,t) = xe^{-t}$.

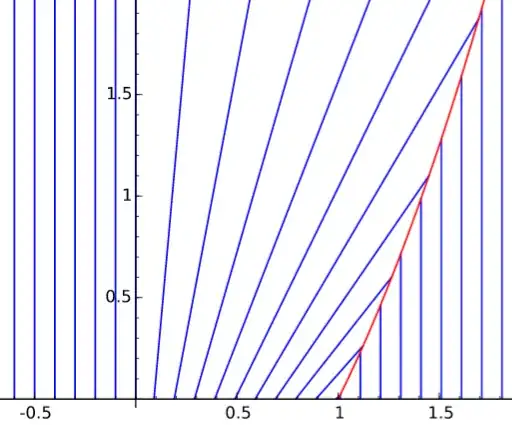
But, the density ($\rho$) goes to $0$ at $x>1$, so how do I treat the moving shock? It obviously does not decay to $0$ at $x=1$ because then conservation would not hold.

mfordcc7
  • 13

1 Answers1

4

The computation $$\dfrac{dx}{dt}=x \rightarrow \dfrac{dx}{x} = dt \rightarrow \ln(x) = t +c \rightarrow x= Ae^{t}$$ is invalid. The equation of characteristics is $\frac{dx}{dt} = \rho(x,t)$, not $\frac{dx}{dt} = x$. It's true that $\rho(x,0)=x$ (for $0<x<1$) but it's not true that $\rho(x,t)=x$.

The characteristics of the Burgers equation are straight lines: namely, the characteristic emanating from $(x_0,0)$ has equation $x=x_0+\rho(x_0,0)t$. In your case, this translates into three groups of characteristics:

  1. $x=x_0$, $x_0\le 0$
  2. $x=x_0(1+t)$, $0<x_0\le 1$
  3. $x=x_0$, $x_0>1$

However, the latter two groups intersect, indicating that a shock wave forms at $ x=1$ at the moment $t=0 $. On the diagram, vertical axis is $t$:

intersect

Solving for $x_0$ from the second equation yields $x_0=x/(1+t)$, hence $\rho(x,t)=\rho(x_0,0)=x/(1+t)$. The solution is:

  1. $\rho(x,t)=0$ when $x\le 0$
  2. $\rho(x,t) = x/(1+t)$ when $x>0$ but to the left of shock wave
  3. $\rho(x,t)=0$ to the right of shock wave

The shock wave propagates at the average of the velocities to the left and right. Thus, its position $s(t)$ satisfies $$\frac{ds}{dt} = \frac{s}{2(1+t)},\quad s(0)=1$$ Solving this ODE yields $s = \sqrt{1+t}$.

Draw this trajectory (it's a parabola) and erase extraneous bits of characteristics: they terminate when reaching the shock wave.

shock