Harmonic function and Neumann Compatibility Condition

Question

______________________________________________________________ Conversely, in a different approach using Green's 1st identity, I showed that by choosing v ≡ 1, that the compatibility condition is derived, and so if u is harmonic on Ω, then the integral of the normal derivative over the boundary is equal to zero.

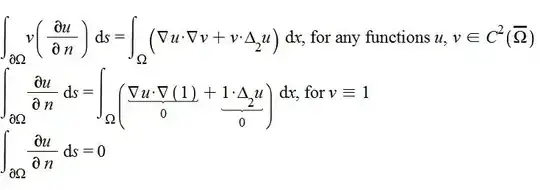______________________________________________________________ However, for circles/balls lying within the closure of the domain (i.e. intersection with the boundary), do I need to use the mean value principle with Green's theorem to prove that u is a harmonic function in Ω?

score 2 · Answer 1 · edited Apr 13 '17 at 12:21

2

Since every open set can be expresses as a countable union of open balls you don't have to deal with intersection of the closure of an open set $\Omega$ with balls.

edited Apr 13 '17 at 12:21

Community

1

answered Nov 04 '15 at 07:57

Michael Medvinsky

5,728

Any other suggestions on how to approach this problem? – Blasius Boundary Layer Nov 04 '15 at 13:50
what else do you looking for? – Michael Medvinsky Nov 04 '15 at 13:53
Ok, so to prove that u is harmonic in Ω, we must show that u satisfies the Laplacian on the boundary. By the given condition, u and its first two derivatives are continuous in Ω. – Blasius Boundary Layer Nov 04 '15 at 20:47
1

In general, the definition of harmonic function is that applying Laplacian on it you get zero. – Michael Medvinsky Nov 04 '15 at 20:52

score 1 · Answer 2 · answered Nov 04 '15 at 21:16

To show that u satisfies the Laplacian, we use Green's 1st identity to obtain the inside-outside theorem equality, setting another arbitrary function, v, contained in the same space as u.

Then, we set v = 1 and obtain an new (simplified) expression of Green's first identity. Hence, for an arbitrary circle B lying in Ω closure, with the compatibility condition = 0, then the integral of the Laplacian = 0. Thus, it follows that the Laplacian = 0 and so the second condition of u being harmonic in Ω is satisfied.

Harmonic function and Neumann Compatibility Condition

2 Answers2