What is the intuitive way to understand Dot and Cross products of vectors?

Question

Suppose, we are crossing a river with heavy current using a speed-boat.

If $x$ is the vector for the current and $y$ is the vector for the speed-boat, then what do $x \cdot y$ and $x \times y$ represent?

Answer 1

The dot product is used when you want the magnitude of the projection of one vector onto another.

For example, consider a one-armed, very sunburned man who's naked pulling a heavy object along the ground by a cord

In this situation the work done by the man is just the projection of the force ($\vec a$) he's providing onto the direction of motion of the object ($\vec b$) times the distance it travels ($\vec b$). Thus the work is $W=\left[\|\vec a\|\cos(t)\right]\|\vec b\| = \vec a \cdot \vec b$.

Here's another example, consider a solar panel:

The amount of solar energy absorbed by the panel depends on the angle between the normal vector from the panel and the sun rays. I.e. the energy is proportional to the dot product of the vector pointing from the sun to the panel and the normal vector from the panel. So if the Sun is straight up you'll get the most energy from the solar panel if it is positioned so that it's normal vector is straight up as well. That's why large solar panel banks often have motors that tilt the panels as the Sun is moving across the sky -- that way they get the most energy they can all day long.

---

The cross product has two purposes. The magnitude of the vector $\vec a \times \vec b$ is the magnitude of the rejection of $\vec a$ from $\vec b$ times the magnitude of $\vec b$ (compare this to the dot product which gives the magnitude of the projection times distance). And its direction is perpendicular to both $\vec a$ and $\vec b$.

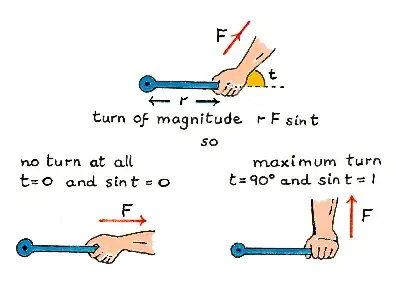
For an application based on the magnitude, consider torque:

The magnitude of the torque on the end of a lever (whose other end is fixed to an object) is given by the rejection of the force vector from the distance vector along the lever times the distance along the lever. So $T = \|\vec F \times \vec r\| = \left[\|\vec F\|\sin(\theta)\right]\|\vec r\|$.

An application of the cross product that uses the fact that the direction is perpendicular to the directions of the input vectors is that of magnetic force.

It can be empirically determined that the magnetic force on a charged particle is in the direction that is perpendicular to both the instantaneous velocity ($\vec v$) AND the magnetic field vector ($\vec B$) acting on that particle in that instant. So it should come as no shock that the mathematical formula we use to calculate the magnetic force is just the cross product of $\vec v$ and $\vec B$ scaled by some number $q$ (which represents the charge of the particle): i.e. $\vec F_m = q(\vec v \times \vec B)$ .

---

For more examples dealing with the dot and cross products, see $[1]$, $[2]$, and $[3]$.

For more information about the mathematical properties of the dot and cross products, I wrote a rather lengthy answer a while back that you might find worth reading.

Answer 2

As per your comment,
$x\cdot y$ represents the projection of the current velocity along the speed-boat velocity.
$x\times y$ represents a vector perpendicular to the plane containing $x$ and $y$ and its direction will be determined by the Right Hand Grip Rule.

Edit: 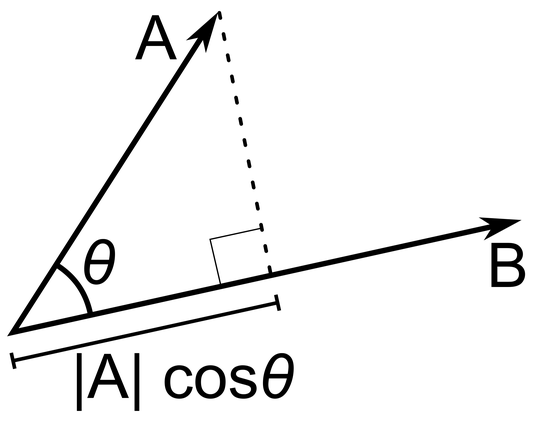This is the projection of a vector on another i.e. use of dot product.

And for cross product, take this example of how a torque works: