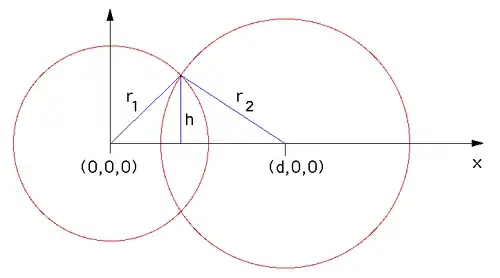
I got to know how to modify formula for radius of circle formed after intersection of two spheres when centres of both spheres where at origin or at x axis to centres at any arbitary positions $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ from previous question.
I was able to understand these: $$h^2 = \frac{4 d^ 2 r1^2 - (d^2 - r2^2 + r1^2)^2}{ 4 d^2}$$
where
$$d^2=(x2-x1)^2+(y2-y1)^2+(z2-z1)^2$$
The equation of circle after intersection of spheres with centres at $(0,0,0)$ and $(d,0,0)$ is $$x=\frac{d^2-r1^2+r2^2}{2d}$$ and parallel to $yz$ plane: $$y^2+z^2=\frac{4 d^2 r2^2-(d^2-r1^2+r2^2)^2}{4 d^2}$$
How could i modify this equation when centres of spheres are at $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$.?