2

I have read much about intersection of two spheres from spheres-intersect , circlesphere and collision-points but all are based on the assumption of spheres located at origin or $x$-axis or some have provided equations in vector form which is far from my ability to understand.

Pre-requisite:

Equation for intersection of two spheres having centres at $(0,0,0)$ and $(d,0,0)$.

$$h^2 = \frac{4 d^ 2 r1^2 - (d^2 - r2^2 + r1^2)^2}{ 4 d^2}$$
where $h$ is radius of intersecting circle.

How can I modify this equation for calculating radius $h$ for spheres intersection having arbitary points as centres $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ (have to convert it into code)?

Glorfindel
  • 3,955
wrangler
  • 123
  • You could translate and then rotate the coordinate system. – coffeemath Oct 28 '15 at 15:10
  • @coffeemath i could translate any one centre other will still be in x,y,z form...... – wrangler Oct 28 '15 at 15:15
  • Yes that's why a rotation is needed. You can calculate the distance d between the centers of the spheres, then translate so one center is at (0,0,0), finally rotate in 3-d so the other center winds up at (d,0,0). At this point apply the equation you have, then reverse the rotation and translation. However it might be a lot easier just to work with the initial centers and radii of the two spheres. – coffeemath Oct 28 '15 at 15:44

2 Answers2

1

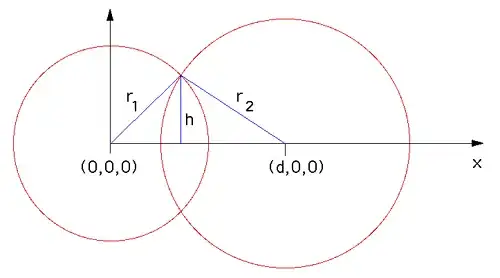
If you forget about the coordinates for a second, you will see that the radius $h$ only depends on the two radii, which are given, and the distance $d$ between the two center points.

Let's change notation and call the two points $x = (x_1,x_2,x_3)$ and $y = (y_1,y_2,y_3)$.

All you need then is to be able to calculate the distance between two arbitrary points. For this, just use Pythagoras:

$d^2 = (y_1-x_1)^2 + (y_2-x_2)^2 + (y_3-x_3)^2$

and plug in the value in the formula you already have.

The set of points you are trying to find is a circle of radius $h$, perpendicular to the line between your two points.

The line between your two points is the set of points with coordinates:

$ x + t(y-x) = \big( (1-t)x_1 + t y_1, (1-t)x_2 + t y_2,(1-t)x_3 + t y_3 \big)$

for $0\leq t \leq 1$. By trigonometry you will see that the coordinates of the center of the circle you are looking for are given by $z = x+t_h(y-x)$ with

\begin{equation}t_h = \frac{\sqrt{r_1^2-h^2}}{d}\end{equation}

The last step is to calculate the coordinates of the circle. They lie on the plane through $z$ which is perpendicular to y-x. So they will be of the form $a = z + b$, where $b$ satisfies: \begin{align} b \circ (y-x) &:= b_1(y_1-x_1) + b_2(y_2-x_2) b_2(y_2-x_2) = 0 \\ ||b||^2 &:= b_1^2 + b_2^2 + b_3^2 = h^2 \end{align}

These can be found here.

Andrea
  • 2,433
1

Actually what you just miss is the distance between the two centers.

Having the sphere located on $(0,0,0)$ or on the x axis does not change the result (you can imagine turning the spheres in space, h does not change).

So you have $d^2=||(x_1,y_1,z_1)-(x_2,y_2,z_2)||^2=(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2$.

Then replace d in the equation and you have h.

Gibe
  • 23