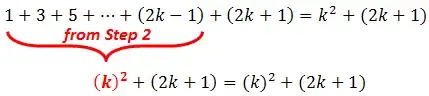Trapped in Induction, how to get out?

Question

Example 1:

Prove by induction that $1+3+5+...+(2n-1)=n^2 \text{ for all } n \in \mathbb{N}....(*)$

Proof:

Step 1: For $n=1$, left-side we have $(2(1)-1) = 1$. Right-side we have $(1)^2 = 1$.

Step 2: Suppose (*) is true for some $n=k \in \mathbb{N}$ that is $$1+3+5+...+(2k-1)=k^2$$

Step 3: Prove that (*) holds true for $n=k \in \mathbb{N}$ that is (adding $(2k+1)$ to both sides) $$1+3+5+...+(2k-1)+(2k+1)=(k)^2+(2k+1)$$

we have

which shows both sides are equal?

but you can do this to several number of problems....

Example 2:

Prove by induction that $1^3+2^3+...+n^3=(1+2+...+n)^2 \text{ for all } n \in \mathbb{N}....(*)$

Proof:

Step 1: For $n=1$, left-side we have $1^3 = 1$. Right-side we have $(1)^2 = 1$. Which shows both sides are true.

Step 2: Suppose (*) is true for some $n=k \in \mathbb{N}$ that is $$1^3+2^3+...+k^3=(1+2+...+k)^2$$

Step 3: Prove that (*) holds true for $n=k \in \mathbb{N}$ that is (adding $(k+1)^3$ to both sides) $$1^3+2^3+...+k^3 + (k+1)^3=(1+2+...+k)^2 + (k+1)^3$$

we have

which shows both sides are equal again...

what am I fundamentally doing wrong?

Answer 1

The problem is that you used the Step 2 too many times :

I'll explain it for the first example :

So you know that $$1+3+\ldots +(2k-1)=k^2$$ . Now add $2k+1$ (as you did) :

$$1+3+\ldots+(2k-1)+(2k+1)=k^2+2k+1$$ this is already true because you assumed it . You don't need to prove it . What you need to really prove is that : $$1+3+\ldots+(2k+1)=(k+1)^2$$ for the inductive step to follow . But you already known that the sum is $k^2+2k+1$ so all you need to prove is that :

$$k^2+2k+1=(k+1)^2$$ which should be obvious .

Answer 2

In Step 3 of the second example, you write "Prove that (*) holds true for $n = k \in N$", but that should be $n = k + 1$.

I find it useful in proofs like this to write down something I call $P(n)$, the proposition that I want to prove, which is typically meant to be true for every integer $n$. In your example 3, $P(n)$ is the statement

$$ 1^3+2^3+...+n^3=(1+2+...+n)^2 $$ That means that $P(1)$ is the statement $$ 1^3=(1)^2 $$ and $P(2)$ is the statement $$ 1^3 + 2^3=(1+2)^2 $$ and so on.

Now you can say this:

I'm going to assume that for some $k \in \mathbb N$, $P(k)$ is true, i.e., that $$ 1^3+2^3+...+k^3=(1+2+...+k)^2 $$ And using only algebraic manipulation, I'll use this to establish that $P(k+1)$ is true, i.e., that $$ 1^3+2^3+...+k^3 + (k+1)^3=(1+2+...+k + (k+1))^2. $$

Now you have a starting point and a clear goal.

I'd say, at this point:

From the hypothesis, we have $$ 1^3+2^3+...+k^3=(1+2+...+k)^2 $$ Adding $(k+1)^3$ to each side, we get $$ 1^3+2^3+...+k^3+ (k+1)^3=(1+2+...+k)^2 + (k+1)^3 $$ To finish the proof, we have to show that the right hand side is the same as $(1 + 2 + \ldots + (k+1))^2$. To do so, let's look at the difference between these two, \begin{align} S &= (1+2+...+k)^2 + (k+1)^3 - ((1+2+...+k+(k+1))^2) \end{align} If we can show $S = 0$, we're done. Well, \begin{align} S &= (1+2+...+k)^2 + (k+1)^3 - ((1+2+...+k+(k+1))^2)\\ &= (1+2+...+k)^2 - (1+2+...+k+(k+1))^2 + (k+1)^3 \end{align} The first two terms look like $A^2 - B^2 = (A-B)(A+B)$, so \begin{align} S &= (1 + 2 + \ldots + k)^2 - (1 + 2 + \ldots + k+(k+1))^2 + (k+1)^3 \\ &= ((1 + 2 + \ldots + k) - (1 + 2 + \ldots + k+(k+1)))\cdot((1 + 2 + \ldots + k) + (1 + 2 + \ldots + k + (k+1))) + (k+1)^3 \\ &= ((1 + 2 + \ldots + k) - (1 + 2 + \ldots + k +(k+1)))\cdot((1 + 2 + \ldots + k) + (1 + 2 + \ldots + k + (k+1))) + (k+1)^3 \\ &= -(k+1)\cdot(2 (1 + 2 + \ldots + k) + (k+1)) + (k+1)^3 \\ &= -(k+1)\cdot(2 \frac{k(k+1)}{2} + (k+1)) + (k+1)^3 \\ &= -(k+1)\cdot( k(k+1) + (k+1)) + (k+1)^3 \\ &= -(k+1)\cdot( k(k+1) + 1\cdot(k+1)) + (k+1)^3 \\ &= -(k+1)\cdot( (k+1)(k+1) ) + (k+1)^3 \\ &= -(k+1)^3 + (k+1)^3 \\ &= 0. \end{align}

Answer 3

What am I fundamentally doing wrong?

There is really only one thing I can tell you are doing wrong, but it is not such a trivial point. Suppose your statement to prove is $S(n)$; the inductive hypothesis will be $S(k)$ (where this will be assumed to be true for some fixed $k\geq ?$), and you will then be trying to show that $S(k)\to S(k+1)$, where you work from the left-hand side of $S(k+1)$ to the right-hand side of $S(k+1)$. The problem is that you are not working to the right-hand side of $S(k+1)$. You simply throw in your extra summand in both examples but do not actually work towards coaxing the right-hand side of $S(k+1)$ out of the left-hand side of $S(k+1)$. To illustrate specifically what I am talking about, I'll show you via your first example (the same applies for your second example though).

---

Example 1: Here you are trying to establish that $$ S(n) : \sum_{i=1}^n(2i-1)=n^2. $$ Your inductive hypothesis is $$ S(k) : \sum_{i=1}^k(2i-1)=k^2. $$ Now, you need to show that $$ S(k+1) : \sum_{i=1}^{k+1}(2i-1)=(k+1)^2 $$ follows from $S(k)$. What you are doing is simply slapping on the extra $2k+1$ term on the left- and right-hand side of $S(k+1)$. This may not be seen as technically wrong in that it will ruin your proof, but it is very sloppy and should be avoided. In a simple summation problem like this, there's not much of an issue, but it's a bad habit to cultivate (the bad habit being not formulating the inductive proof very clearly). Here, we clearly have that $k^2+2k+1=(k+1)^2$, but what happens when you have something much more complicated? You end up with an unnecessarily complicated proof that is sloppy, unclear, etc. Here is how I would write up your proof:

Claim: For $n\geq 1$, let $S(n)$ denote the proposition $$ S(n) : \sum_{i=1}^n(2i-1)=n^2. $$

Base case ($n=1$): $S(1)$ says that $2(1)-1=1=1^1$, and this is true.

Inductive step: Assume that $$ S(k) : \sum_{i=1}^k(2i-1)=k^2 $$ is true for some fixed $k\geq1$. To be shown is that $$ S(k+1) : \sum_{i=1}^{k+1}(2i-1)=(k+1)^2 $$ follows. Beginning with the left-hand side of $S(k+1)$, \begin{align} \sum_{i=1}^{k+1}(2i-1)&= \sum_{i=1}^k(2i-1)+2(k+1)-1\tag{by $\Sigma$-defn.}\\[0.5em] &= k^2+(2k+1)\tag{by $S(k)$}\\[0.5em] &= (k+1)^2\tag{factor} \end{align} we end up at the right-hand side of $S(k+1)$, completing the inductive step.

By mathematical induction, the proposition $S(n)$ is true for all $n\geq 1$. $\blacksquare$

---

Finally, you may find this post helpful in regards to writing clear induction proofs.