11

Let $a,b,c$ be nonnegative real numbers and $a+b+c=3$. Prove the inequality $$ \sqrt{24a^2b+25}+\sqrt{24b^2c+25}+\sqrt{24c^2a+25}\le 21 $$

I have tried to find the solution using classical inequalities, but failed. Any idea?

Michael Rozenberg
  • 194,933
Booldy
  • 1,070
  • But what have you done ? – callculus42 Aug 29 '15 at 03:36
  • tried to apply all kind of classical inequalities,Cauchy,Holder,Jensen,Minkowski,...,but doesnt work – Booldy Aug 29 '15 at 03:38
  • @calculus it's somewhat difficult to make progress on contest problems in inequalities when there are usually only 2 or 3 ways of tackling it. – user217285 Aug 29 '15 at 03:38
  • i suppose it is so,but someone might have an idea which leeds to a solution – Booldy Aug 29 '15 at 03:40
  • try to use the Lagrange Multiplier method – Dr. Sonnhard Graubner Aug 29 '15 at 08:58
  • 2
    From symmetry you might expect the a=b=c=1 to be a critical point of the right hand side. By inspection, it gives equality in the inequality. Thus you might check this as well. – kodlu Aug 29 '15 at 10:35
  • The best way is what @kodlu said, check the corners (3,0,0) and the middle (1,1,1). The trick is then, to rigorously prove there are no extremal points between them, or if they are, they are not maxima. You can observe the values of $a^2b$ on triangle $a+b+c=3$, and work from there. – orion Aug 29 '15 at 10:54
  • 6
    unfortunetly nobody reads the comments,equality holds at $(1,1,1)$ and $(2,1,0)$ and its cyclic permutations – Booldy Aug 29 '15 at 12:53
  • 3
    I'm just wondering: where do you have the inequality from? – Redundant Aunt Aug 29 '15 at 12:55
  • it is mine,i have a kind of solution but it requires a lot of calculation and it is really uggly.Now i will post helping inequality maby someone has a nice solution for that – Booldy Aug 29 '15 at 12:57
  • I think, that we have generally $\sum_{cyc}{\sqrt{x a^2b+y}≤\max{\left(3\sqrt{x+y},\sqrt{4x+y}+2\sqrt{y}\right)}}$. – Redundant Aunt Aug 29 '15 at 17:29

2 Answers2

5

Proof without words (more like a pictural comment). The following reference gives some clues about the know how to do such a thing:

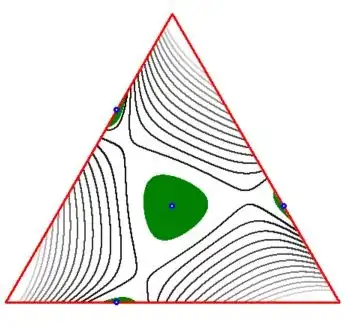
enter image description here         enter image description here

Define the function to be investigated as: $$ F(a,b,c) = \sqrt{24a^2b+25}+\sqrt{24b^2c+25}+\sqrt{24c^2a+25} - 21 $$ Scanning the inside of the triangle (picture on the left) pixel by pixel (i.e. numerically) reveals that: 

minimum = -5.97874499595267E+0000 ; maximum = -1.86093567294196E-0005
The exact minimum is at the vertices of the triangle: $F(3,0,0)=F(0,3,0)=F(0,0,3)=-6$ , just beyond reach of the numerics.
Contour lines of the function are shown in the picture on the right. They are at: 
for g := 1 to 16 do
begin
  level := -sqr(g/8); { level = minus g/8 squared }
More black means closer to the maximum. Of course we already know that: $$ F(1,1,1) = 0 \; ; \; F(2,1,0) = 0 \; ; \; F(0,2,1) = 0 \; ; \; F(1,0,2) = 0 $$ These places are indicated as $\color{blue}{blue}$ spots in the picture on the right. So there is strong evidence (ipse est NO "rigorous proof") that $0$ is indeed the maximum. My 2 cents worth ..

EDITs. Picture on the right augmented with $\color{green}{green}$ areas where $|F(a,b,c)| < 0.1$ .
If $F(a,b,c)$ is specified for an edge of the equilateral triangle, then we can do some analytical work, though it remains a modest attempt: $$ f(x) = F(3-x,x,0) = \sqrt{24(3-x)^2x+25}-11 $$ Derivative zero: $$ f'(x) = \frac{1}{2}24\frac{-2(3-x)x+(3-x)^2}{\sqrt{24(3-x)^2x+25}} = 0 \quad \Longleftrightarrow \quad x\in\{3,1\} $$ Giving the known minimum $F(0,3,0)$ and the known maximum $F(2,1,0)$ , the only difference being that these are now proven unique, at the triangle's edges.
In order to demonstrate that the problem is "not so easy", let's specify again, for a line through one vertex of the triangle $(3,0,0)$ and the midpoint $(1,1,1)$: $$ g(x) = F(3-2x,x,x) = \sqrt{24(3-2x)^2x+25}+\sqrt{24x^3+25}+\sqrt{x^2(3-2x)+25}-21 $$ Then we already know that a solution of $g'(x)=0$ is given by $F(1,1,1)=0$. But, if this is fed into MAPLE , then all I've got is a seemingly endless loop: 

> solve(diff(g(x),x)=0,x);
Warning, computation interrupted
Han de Bruijn
  • 17,070
  • 1
    A plausability check of this situation via Wolfram Alpha is affirmative. Regrettably, an analytic proof looking for local maxima and maxima at the boundaries seems to be rather cumbersome. In fact, I would really appreciate if someone could provide a technique based upon clever manipulations using inequalities. – Markus Scheuer Sep 06 '15 at 22:07
2

By C-S $$\left(\sum_{cyc}\sqrt{24a^2b+25}\right)^2\leq\sum_{cyc}(24a^2b+25)(a+3b+5c)\sum_{cyc}\frac{1}{a+3b+5c}$$ Thus, it remains to prove that $$\sum_{cyc}(24a^2b+25)(a+3b+5c)\sum_{cyc}\frac{1}{a+3b+5c}\leq441$$ or $$\sum_{cyc}(648a^2b+25(a+b+c)^3)(a+3b+5c)\sum_{cyc}\frac{1}{a+3b+5c}\leq441(a+b+c)^3$$ or $$\sum_{cyc}(20a^6+47a^5b+352a^5c-209a^4b^2+509a^4c^2-275a^3b^3+$$ $$+690a^4bc-556a^3b^2c-143a^3c^2b-435a^2b^2c^2)\geq0.$$ Now, let $a=\min\{a,b,c\}$, $b=a+u$ and $c=a+v$.

Hence, we need to prove that $$4779(u^2-uv+v^2)a^4+27(263u^3-211u^2v+130uv^2+263v^3)a^3+$$ $$+9(365u^4-58u^3v-453u^2v^2+965uv^3+365v^4)a^2+$$ $$+3(173u^5+169u^4v-739u^3v^2+356u^2v^3+1156uv^4+173v^5)a+$$ $$+(u-2v)^2(20u^4+127u^3v+219u^2v^2+93uv^3+5v^4)\geq0,$$ which is obvious.

Done!

Michael Rozenberg
  • 194,933