Math Intuition and Natural Motivation Behind t-Student Distribution

Question

I am trying to understand with basic mathematical background how the $t$-Student distribution is a "natural" pdf to define. A more accessible explanation than this post, or the daunting Biometrika paper by RA Fisher.

Background:

The central limit theorem states that if ${\textstyle X_{1},X_{2},...,X_{n}}$ are each a random sample of size ${\textstyle n},$ taken from a population with mean ${\textstyle \mu }$ and finite variance ${\textstyle \sigma ^{2}}$ and if ${\textstyle {\bar {X}}}$ is the sample mean, then the limiting form of the distribution of ${\textstyle Z=\left({\frac {{\bar {X}}_{n}-\mu }{\sigma /\surd n}}\right)}$ as ${\textstyle n\to \infty },$ is the standard normal distribution.

If $X_1, \ldots, X_n$ are iid random variables $\sim N(\mu,\sigma^2)$,

$$\frac{\bar{X}\,-\,\mu}{\sigma/\sqrt{n}} \sim N(0,1)$$

This is the basis of the Z-test, $Z=\frac{\bar{X}\,-\,\mu}{\sigma/\sqrt{n}}$

[Note that the preceding opening statement is now correct after reflecting @Ian and @Michael Hardy comments to the OP in reference to the CLT.]

If the standard deviation of the population, $\sigma$, is unknown we can replace it by the estimation based on a sample, $S$, but then the expression (one-sample t-test statistic) will follow a $t$-distribution:

$$ t=\frac{\bar{X}\,-\,\mu}{S/\sqrt{n}}\sim t_{n-1}$$

with $$s=\sqrt{\frac{\sum(X_i-\bar X)^2}{n-1}}.$$

Minimal manipulations of this equation for $T$

$$\begin{align} \frac{\bar{X}\,-\,\mu}{S/\sqrt{n}} &= \frac{\bar{X}\,-\,\mu}{\frac{\sigma}{\sqrt{n}}} \frac{1}{\frac{S}{\sigma}}\\[2ex] &= Z\,\frac{1}{\frac{S}{\sigma}}\\[2ex] &= \frac{Z}{\sqrt{\frac{\color{blue}{\sum(X_i-\bar X)^2}}{(n-1)\,\color{blue}{\sigma^2}}}}\\[2ex] &\sim\frac{Z}{\sqrt{\frac{\color{blue}{\chi_{n-1}^2}}{n-1}}}\\[2ex] &\sim t_{n-1}\small \tag 1 \end{align}$$

will introduce the chi square distribution, $(\chi^2).$

The chi square is the distribution that models $X^2$ with $X\sim N(0,1)$:

Let's say that $X \sim N(0,1)$ and that $Y=X^2$ and find the density of $Y$ by using the $\text{cdf}$ method:

$$\Pr(Y \leq y) = \Pr(X^2 \leq y)= \Pr(-\sqrt{y} \leq x \leq > \sqrt{y}).$$

We cannot integrate in close form the density of the normal distribution. But we can express it:

$$ F_X(y) = F_X(\sqrt{y})- F_X(-\sqrt[]{y}).$$ Taking the derivative of the cdf:

$$ f_X(y)= F_X'(\sqrt{y})\,\frac{1}{\sqrt{y}}+ > F_X'(\sqrt{-y})\,\frac{1}{\sqrt{y}}.$$

Since the values of the normal $\text{pdf}$ are symmetrical:

$$ f_X(y)= F_X'(\sqrt{y})\,\frac{1}{\sqrt{y}}.$$

Equating this to the $\text{pdf}$ of the normal (now the $x$ in the $\text{pdf}$ will be $\sqrt{y}$ to be plugged into the $e^{-\frac{x^2}{2}}$ part of the normal $\text{pdf}$); and remembering to in include $\frac{1}{\sqrt{y}}$ at the end:

$$\begin{align} f_X(y) &= F_X'\left(\sqrt{y}\right)\,\frac{1}{\sqrt[]{y}}\\[2ex] &=\frac{1}{\sqrt{2\pi}}\,e^{-\frac{y}{2}}\, \frac{1}{\sqrt[]{y}}\\[2ex] &=\frac{1}{\sqrt{2\pi}}\,e^{-\frac{y}{2}}\, y^{\frac{1}{2}- 1} \end{align}$$

Comparing to the pdf of the chi square:

$$ f_X(x)= \frac{1}{2^{\nu/2}\Gamma(\frac{\nu}{2})}e^{\frac{-x}{2}}x^{\frac{\nu}{2}-1}$$

and, since $\Gamma(1/2)=\sqrt{\pi}$, for $\nu=1$ df, we have derived exactly the $\text{pdf}$ of the chi square.

---

In the case of the $t$-distribution the chi-square is suitable to model the sum of squared normals, i.e $\displaystyle \sum(X_i-\bar X)^2 $ in the set of Eq $(1),$ a well known property derived here typically with $n$ degrees of freedom, but

why is it $n\,-\,1$ here, i.e. $\color{blue}{\chi^2_{n-1}}$ in eq. $(1)$?

I don't know how to explain $\sigma^2$ in $\frac{\sum(X_i-\bar X)^2}{\sigma^2}$ in equation $(1)$ becoming "absorbed" into the $\chi_{n-1}^2$ part of the $\text{t-Student's pdf}.$

So it boils down to understanding why

$$\frac 1 {\sigma^2} \left((X_1-\bar X)^2 + \cdots + (X_n - \bar X)^2 \right) \sim \chi^2_{n-1}.$$

After that the derivation of the pdf is not that daunting.

---

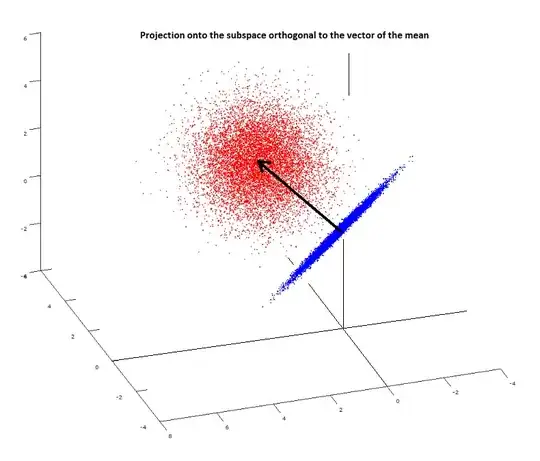
PS: The accepted answer below becomes clear after reading this Wikipedia entry. Also, a plot may be useful including the spherical cloud $(X_1,X_2,X_3)$ (in red) with the orthogonal projection, $(X_1-\bar X,\ldots,X_n-\bar X),$ on the $n-1$ subspace forming a plane (in blue) at the origin:

Answer 1

You wrote "which is an expression of the central limit theorem". That is not correct. You started with a normal distribution. The central limit theorem says if you start with any distribution with finite variance, not assumed to be normal, the sum of i.i.d. copies will be nearly normally distributed.

Your main question seems to be: how does the chi-square distribution get involved?

You have $X_1,\ldots,X_n\sim\text{ i.i.d. } N(\mu,\sigma^2)$ and $\bar X = (X_1+\cdots+X_n)/n$. The proposition then is $$ \frac 1 {\sigma^2} \Big((X_1-\bar X)^2 + \cdots + (X_n - \bar X)^2 \Big) \sim \chi^2_{n-1}. $$

The random variables $(X_i - \bar X)/\sigma$ are not independent, but have covariance $-1/n$ between any two of them.

The standard deviation of each of them is not $1$, but $\sqrt{(n-1)/n\,{}}$.

There are not $n-1$ of them, but $n$.

But the distribution of the sum of their squares is asserted to be the same as if they were (1) independent and (2) each has standard deviation $1$ and (3) there are $n-1$ of them.

This can be understood geometrically, as follows: The mapping $(X_1,\ldots,X_n)\mapsto (\bar X, \ldots, \bar X)$ is the orthogonal projection onto a $1$-dimensional subspace of $\mathbb R^n$, and it complementary mapping $(X_1-\bar X,\ldots,X_n-\bar X)$ is the orthogonal projection onto the $(n-1)$-dimensional subspace defined by the constraint that the sum of the coordinates is $0$. Notice that the latter projection takes the mean vector $(\mu,\ldots,\mu)$ to $(0,\ldots,0)$.

The distrbution of $(X_1,\ldots,X_n)$ is spherically symmetric about the mean vector, since it is $$ \text{constant}\cdot \exp\left( -\frac 1 2 \sum_{i=1}^n\left( \frac{x_i-\mu} \sigma \right)^2 \right)\,dx_1\,\cdots\,dx_n. $$

The distribution of an orthogonal projection of this random vector, which projection takes the mean vector to $0$, is spherically symmetric about $0$ in the lower-dimensional space onto which one projects. So let $(U_1,\ldots,U_{n-1})$ be the coordinates of $(X_1-\bar X,\ldots, X_n-\bar X)$ relative to some orthonormal basis of that $(n-1)$-dimensional subspace, and then you have $$ (X_1-\bar X)^2 + \cdots + (X_n-\bar X)^2 = U_1^2 + \cdots + U_{n-1}^2 \tag 1 $$ and $$ U_2,\ldots,U_n\sim\text{ i.i.d. }N(0,\sigma^2). $$

Therefore $(1)$ is distributed as $\sigma^2\chi^2_{n-1}$.

Also, notice that $\bar X$ is actually independent of $(X_1 - \bar X,\ldots,X_n-\bar X)$. That follows from the fact that they are jointly normally distributed and $\operatorname{cov}(\bar X, X_i-\bar X)=0$. That is also needed in order to conclude that you get a $t$-distribution.

PS: One can do this with matrices: There is an $n\times n$ matrix $Q$ for which $$ QX=Q\begin{bmatrix} X_1 \\ \vdots \\ X_n \end{bmatrix} = \begin{bmatrix} X_1 - \bar X \\ \vdots \\ X_n - \bar X \end{bmatrix}. $$ It satisfies $Q^2=Q^T=Q$. And $P=I-Q$ satisfies $P^2=P^T=P$, and $QP=PQ=0$. Then we have $$ \operatorname{cov}(PX, QX) = P\Big(\operatorname{cov}(X,X)\Big) Q^T = P(\sigma^2 I)Q^T = \sigma^2 PQ = 0. $$ and $$ QX \sim N(0,\sigma^2 Q\Big(\sigma^2 I\Big) Q^T) = N(0,\sigma^2 Q). $$ (We get $0$ as the mean hear because $Q$ times the mean vector is $0$.) Our denominator in the $t$-statistic is then $\|QX\|/\sqrt n$.

PS: Here's somewhat different way of expressing it. The vector $(X_1,\ldots,X_n)$ has expected value $(\mu,\ldots,\mu)$. Let $(U_1,\ldots,U_{n-1},U_n)$ be the coordinates of the point $(X_1,\ldots,X_n)$ in a different coordinate system: The $n$th component $U_n$ is the position on an axis pointing from $(0,\ldots,0)$ in the direction of $(\mu,\ldots,\mu)$, and let the other $U_k$, for $k=1,\ldots,n-1$ are components in directions at right angles to that one. In the first coordinate system, the projection of $(X_1,\ldots,X_n)$ onto the space in which the sum of the components is $0$ is $(X_1-\bar X,\ldots,X_n-\bar X)$. In the second coordinate system the projection of $(U_1,\ldots,U_{n-1},U_n)$ onto that same space is $(U_1,\ldots,U_{n-1},0)$. Transforming $(\mu,\ldots,\mu)$ into the second coordinate system, we get $(0,\ldots,0,\mu\sqrt n)$, and the projection of that onto the aforementioned subspace is $(0,\ldots,0,0)$. Hence $(X_1-\bar X)^2+\cdots+(X_n-\bar X)^2 = U_1^2+\cdots+U_{n-1}^2$ and $U_1,\ldots,U_{n-1}\sim\text{ i.i.d. } N(0,\sigma^2)$.