-1

I recently bumped into this question which asks why $\pi=4$ is wrong.

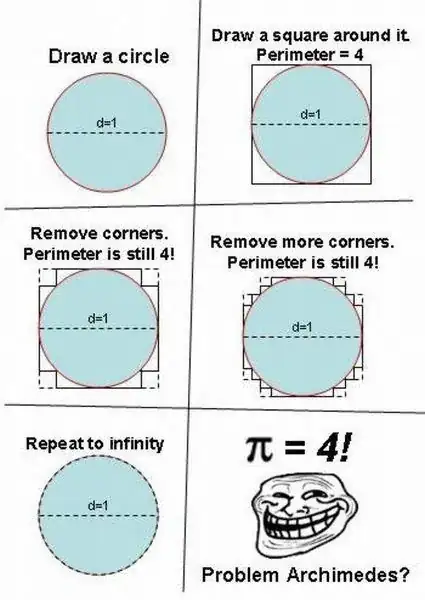
enter image description here

And some answers(see the answer of user TCL, for example) stated that this has to do with functions and their derivatives.

Their answers were something like this:

Let $F_n(x)$ be a sequence of curves (the zigzag curves in the above picture) that approach $g(x)$ as n tends to $\infty$.

And $g(x)$ the curve that represents the circle.

$$\lim_{n \to \infty} F_n(x) = g(x).$$

Does not imply

$$\lim_{n \to \infty} F'_n(x) = g'(x).$$

And lengths has to do with derivatives($\int \sqrt{f'(x)+1} \, dx$), therefore convergence of two curves does not mean convergence of their length.

And based upon my understanding of this:

enter image description here

the condition that the function should satisfy for the above implication to hold is that it has to be a continuous function,but the curve(see the linked question) approximating the circle it is not continuous.

Is my understanding correct?

Does convergence of two continuous functions implies the convergence of their derivatives?

If this is the case, then why the function that approximates the circles is not continuous?

I saw this question, But I don't know if its related to my question about continuity?

Community
  • 1
Omar Nagib
  • 1,258
  • what derivatives? – Asinomás Jul 19 '15 at 05:27
  • @dREaM If you have a curve that is given by $f(x)$, its length is computed by $\int \sqrt{f'(x)+1} dx$ – Omar Nagib Jul 19 '15 at 05:28
  • 1
    there are continuous functions that are nowhere differentiable. – Asinomás Jul 19 '15 at 05:28
  • What are "two continous functions"? Your question seems unclear – Michael Galuza Jul 19 '15 at 05:34
  • @MichaelGaluza If $F(x), g(x)$ are continuous, and $\lim_{n \to \infty} F_n(x) = g(x)$, Does that imply $\lim_{n \to \infty} F'_n(x) = g'(x)$? – Omar Nagib Jul 19 '15 at 05:37
  • 1
    Let $F_n(x)=\frac1n\sin(nx)$. Then clearly $F_n(x)\to0$ but $F_n'(x)=\cos(nx)\not\to0$. –  Jul 19 '15 at 05:40
  • I would like to know why my question was downvoted, downvoter can you explain? – Omar Nagib Jul 19 '15 at 06:01
  • 3
    For one, you are confusing the fact that the functional $\gamma\mapsto\ell(\gamma)$ is not continuous (for the uniform norm) wih the fact that one applies $\ell$ to continuous functions. – Did Jul 19 '15 at 06:14
  • @Did I would be pretty grateful if you clear up my confusion and misunderstanding. – Omar Nagib Jul 19 '15 at 06:16
  • @MichaelGaluza No, uniform convergence is not enough. Rahul's counterexample converges uniformly. –  Jul 19 '15 at 06:26
  • @Strants, oh, really. Thanks – Michael Galuza Jul 19 '15 at 06:27
  • Omar: I just did. (Note that there are other misunderstandings such as, possibly, some confusion of continuity with differentiability.) Re the point underlined in my first comment, a productive approach from your part would be to explain what it is you do not understand in it. This would require to read the comment slowly and carefully, nothing more. But then, this applies already to @Emanuele's comment, which is already pretty clear and explicit and precisely stated... – Did Jul 19 '15 at 06:28
  • @Did I know that a function is continuous when $\lim_{n \to c} f(x) = f(c)$. It is differentiable if its continuous and $f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$ exists. Every differentiable $f$ is continuous but the opposite is not true. This is my understanding of the concepts. Now regarding your comment, I didn't understand it at all, I'm totally unfamiliar with the concepts you're talking about. – Omar Nagib Jul 19 '15 at 06:39
  • ?? The only "concept" my first comment is mentioning is continuity (at two levels, continuity of $\gamma$ some function from some interval of $\mathbb R$ to $\mathbb R^2$, and (non-)continuity of $\ell$ some function defined on some space of differentiable functions $\gamma$). – Did Jul 19 '15 at 06:41
  • If you take any number of turns along N-S and E-W roads your distance won't change. But if at all there are diagonal shortcuts, your total length is thereby less, no? – Narasimham Jul 19 '15 at 22:12

2 Answers2

3

No, you misunderstand Emanuele Paolini's answer. He notes the problem that $\ell$ is not a continuous function. But his $\ell$ does not refer to one of the curves, which you label $F_n$ and $g$. Instead, $\ell$ is the function that inputs a curve and outputs its length. What it means for such a "higher-order" function to be continuous or discontinuous takes some work to explain... You can try researching the topology of uniform convergence.

Chris Culter
  • 26,806
  • Alright, that's regarding Emanuele's answer, what about TCL's answer(the second Answer in the linked question)? He states that when two functions converges, this does not imply thier derivatives do. When he's talking about functions, is he talking about the functions that represent the curves or the function which "takes a curve as an input and output its lenght"? – Omar Nagib Jul 19 '15 at 06:29
  • TCL is talking about the curves. Note the sentence "let x=a(t) ... be the parameterizations of the two curves". – Chris Culter Jul 19 '15 at 06:34
  • So based on the answer of TCL, which says that convergence of functions (those representing the curves) does not imply convergence of their derivatives(which are used in computing the length), And this is the reason why the fact that the zigzag approaches the circle does not imply that their length converge. Is my understanding correct? – Omar Nagib Jul 19 '15 at 06:44
  • That's correct! Still, you should be careful not to over-generalize the idea. I'm sure there are other sequences of curves where the derivatives behave very badly yet the lengths still miraculously converge. – Chris Culter Jul 19 '15 at 06:59
  • So what is the neccessary condition that must be satisfied for the implication to holds true? – Omar Nagib Jul 19 '15 at 07:04
  • Well, I doubt that there is any reasonable necessary condition. – Chris Culter Jul 19 '15 at 07:10
1

Let $f(x)=\frac1x\sin x^2$, $g(x)\equiv0$. Then $$ f'(x)=-\frac{1}{x^2}\sin x^2+\frac1x\cdot 2x\cos x^2, $$ which has no limit at infinity, while derivative of $g$ is 0.

Przemysław Scherwentke
  • 13,668
  • 5
  • 35
  • 56