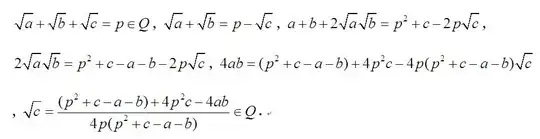Assume that $a，b，c, \sqrt{a}+ \sqrt{b}+\sqrt{c} \in\mathbb Q$ are rational，prove $\sqrt{a},\sqrt{b},\sqrt{c} \in\mathbb Q$,are rational.
I know that can be proved, would like to know that there is no easier way
$\sqrt a + \sqrt b + \sqrt c = p \in \mathbb Q$,
$\sqrt a + \sqrt b = p- \sqrt c$,
$a+b+2\sqrt a \sqrt b = p^2+c-2p\sqrt c$,
$2\sqrt a\sqrt b=p^2+c-a-b-2p\sqrt c$,
$4ab=(p^2+c-a-b)+4p^2c-4p(p^2+c-a-b)\sqrt c$,
$\sqrt c=\frac{(p^2+c-a-b)+4p^c-4ab}{4p(p^2+c-a-b)}\in\mathbb Q$.
[See here and here for an introduction to the proof. They are explicitly worked special cases].
As you surmise, induction works, employing our prior Lemma (case $\rm\,n = 2\,\!).\,$ Put $\rm\,K = \mathbb Q\,$ in
Theorem $\rm\ \sqrt{c_1}+\cdots+\!\sqrt{c_{n}} = k\in K\ \Rightarrow \sqrt{c_i}\in K\,$ for all $\,\!\rm i,\,$ if $\rm\, 0 < c_i\in K\:\!$ an ordered field.
Proof $\, $ By induction on $\:\!\rm n.\,$ Clear if $\rm\,n=1.\,$ It is true for $\rm\,n=2\,$ by said Lemma. Suppose $\rm\, n>2.$ Below we prove $\rm\color{#0af}{one}$ of the square-roots is in $\rm K\:\!$. Hence the sum of all of the others is also in $\rm K,\,$ thus, by induction, all of the others are also in $\rm K,\,$ finishing the proof.
Note that $\rm\,\sqrt{c_1}+\cdots+\sqrt{c_{n-1}}\, =\, k\! -\! \sqrt{c_n}\in K(\sqrt{c_n})\,$ so all $\,\rm\sqrt{c_j}\in K(\sqrt{c_n})\,$ by induction.
Therefore $\rm\, \sqrt{c_j} =\, a_j + b_j\sqrt{c_n}\,$ for some $\rm\,a_j,\,\!b_j\in K,\,$ for $\rm\,j=1,\ldots,n\!-\!1$.
$\rm \color{#0a0}{Some\,\ {b_j < 0}}\,$ $\Rightarrow$ $\rm\ a_j = \sqrt{c_j}-b_j\sqrt{c_n} = \sqrt{c_j}+\!\sqrt{b_j^2 c_n}\in K\,\Rightarrow \color{#0af}{\sqrt{c_j}}\in K\,$ by Lemma $\rm(n\!=\!2).$
Else $\,\rm \color{#90f}{all\ b_j \ge 0},\,$ so $\rm\, b := b_1\!+\cdots+b_{n-1} \ge 0.\,$ Let $\rm\, a := a_1\!+\cdots+a_{n-1}\ $ so $$\rm \sqrt{c_1}+\cdots+\!\sqrt{c_{n}}\, =\, a+(b\!+\!1)\,\sqrt{c_n} = k\in K\,\Rightarrow\,\!\color{#0af}{\sqrt{c_n}}= {\small \frac{\!k\!-\!a}{\color{#c00}{b\!+\!1}}}\in K\quad $$
So in $\rm\color{#0a0}{every}\ \color{#90f}{case}\ \color{#0af}{one}$ of the square-roots lies in $\rm K\,$ (notice that $\rm\,b\ge0\,\Rightarrow \color{#c00}{b\!+\!1}\ne 0).\,$ $\ \bf\small QED$
Remark $ $ The positivity of the summands is crucial (else e.g. $\,-\sqrt{2} + \sqrt{2}\in \mathbb Q\,$ but $\rm\,\sqrt{2}\not\in\mathbb Q).\,$ More generally see this post on the linear independence of square-roots (Besicovic's theorem).
Maybe not easier, but quite elegant :
Suppose that $a,b,c$ are all non zero. Let $K=\mathbb{Q}(\sqrt{a},\sqrt{b},\sqrt{c})$ and $n = [K: \mathbb{Q}]$. Then since $Tr_{K/\mathbb{Q}}(\sqrt{a}) = Tr_{\mathbb{Q}(\sqrt{a})/\mathbb{Q}} \circ Tr_{K/\mathbb{Q}(\sqrt{a})} (\sqrt{a})$, we have $$ Tr_{K/\mathbb{Q}}(\sqrt{a}) = \begin{cases} 0,& \text{if } \sqrt{a} \notin \mathbb{Q} \\ n\sqrt{a}, &\text{if } \sqrt{a} \in \mathbb{Q}, \end{cases}$$ and same for $\sqrt{b}$ and $\sqrt{c}$.
By hypothesis $\sqrt{a} + \sqrt{b} +\sqrt{c} \in \mathbb{Q}$, so $$ Tr_{K/\mathbb{Q}}(\sqrt{a}) + Tr_{K/\mathbb{Q}}(\sqrt{b}) + Tr_{K/\mathbb{Q}}(\sqrt{c}) = n\sqrt{a} + n \sqrt{b} + n \sqrt{c}.$$ It is easy to conclude that $\sqrt{a},\sqrt{b},\sqrt{c} \in \mathbb{Q}$.
