0

How can we solve the equation: $$\sin(\beta/2)=\beta/4$$ where $\beta $ is in radians?

Micah
  • 38,108
  • 15
  • 85
  • 133
Farzin nasiri
  • 11
  • 2
  • 6
    Numerically. By drawing a picture we can roughly pin down the candidates. Then use say the Newton Method. – André Nicolas Jul 16 '15 at 07:24
  • But that's a very hard solution.Isn't there an easier way to solve it? – Farzin nasiri Jul 16 '15 at 07:47
  • you can usualy guess one solution (usualy 0 1, $\pi$ or something like that ) and show that there is no other. in this case one solution is 0 but there are two more and you can obtain them only numerically (drawing a picture can help locating them ) . other two are $x_1$~3.79 and $x_2$~ -3.79 according to wolfram – jack Jul 16 '15 at 07:58
  • I have to solve this eqution to answer one of the problems in(fundamentals of physics) can we solve it using derivative or something like that? It most have a better solution than using a graph or newton method. – Farzin nasiri Jul 16 '15 at 08:22
  • The solutions $\beta \approx \pm 3.79$ and zero are what they are. You can reformulate the problem by setting $x = \beta/2$ and asking for the roots of $\sin x = x/2$, but the answers will come out the same for $\beta$ once you've solved for $x$. – hardmath Jul 18 '15 at 02:25

3 Answers3

4

As André Nicolas commented, there is no analytical solution and numerical methods (such as Newton) should be used.

I cannot resist the pleasure of showing you a $1400$ years old approximation $$\sin(x) \simeq \frac{16 (\pi -x) x}{5 \pi ^2-4 (\pi -x) x}\qquad (0\leq x\leq\pi)$$ proposed by Mahabhaskariya of Bhaskara I, a seventh-century Indian mathematician and astronomer.

Applied to your case, this would lead to the equation $$\frac{8 \left(\pi -\frac{\beta }{2}\right) \beta }{5 \pi ^2-2 \left(\pi -\frac{\beta }{2}\right) \beta }=\frac \beta 4$$ which reduces to a quadratic the solution of it being given by $$\beta=-8+\pi +2 \sqrt{16+(4-\pi ) \pi }\approx 3.78954$$

If you look at this post where I was asking almost the same question, you will see that Christian Blatter proposed for the solution of $\sin(x)=a x$, the following approximation $$x\approx \sqrt{{\pi^2+5.95839 a - 15.828 a^2\over 1 + 2.60371 a + 0.690687 a^2}}$$ which, applied to your case ($x=\frac \beta 2$,$a=\frac 12$), would give $\beta \approx 3.79122$ while, for six significant figures, the solution is $\approx 3.79099$.

Similarly, after Christian Blatter, I made a small improvement using $$x\approx \sqrt{\frac{9.86775+4.91766 a-14.7794 a^2}{1+2.48744 a+0.633963 a^2}}$$ which, applied to your case , would give $\beta \approx 3.79117$.

Community
  • 1
Claude Leibovici
  • 260,315
3

Of course $\beta=0$ is a solution, but I guess you should call it trivial. Setting $\beta/2=x$, you can realize what is going on by looking at the graph of $y=\sin x - \frac{x}{2}$. You will see that two more solutions exist (the function is trivially odd in $x$). You will never find a closed form in terms of elementary functions, so all you can do is to prove that they exist and to estimate them by some numerical method. 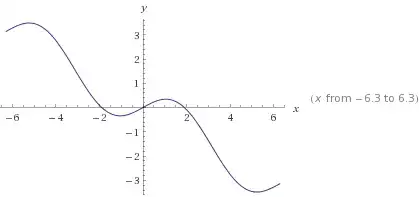enter image description here

Siminore
  • 35,136
0

For $\beta\neq 0$ we have $\text{sinc}\frac{\beta}{2}=\frac{1}{2}$ so $\beta\approx\pm 3.79009$ (according to Wolfram alpha).

J.G.
  • 115,835